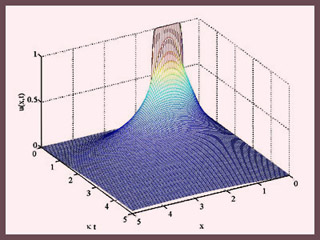
Time evolution of the temperature distribution u(x,t) on a semi-infinite rod whose end (at x=0) is kept at 0. Initially (t=0), the temperature of the rod is 1 between x=0.5 and x=1.5, and is zero everywhere else. (Image by Dr. Matthew Hancock.)
Instructor(s)
Dr. Matthew Hancock
MIT Course Number
18.303
As Taught In
Fall 2006
Level
Undergraduate
Course Description
Course Features
Course Description
This course covers the classical partial differential equations of applied mathematics: diffusion, Laplace/Poisson, and wave equations. It also includes methods and tools for solving these PDEs, such as separation of variables, Fourier series and transforms, eigenvalue problems, and Green's functions.
Other Versions
Other OCW Versions
OCW has published multiple versions of this subject. ![]()
Archived versions: ![]()


