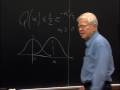Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics covered: Quantization
Instructors: Prof. Robert Gallager, Prof. Lizhong Zheng

Lecture 6: Quantization
NARRATOR: The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.
PROFESSOR: To take up the topic of quantization, you remember we're talking about source coding in the first part of the course, channel coding in the last 2/3 of the course. Source coding, like all, is divided into three parts. If you have waveforms, such as speech, you start out with the waveform.
The typical way to encode waveforms is you first either sample the waveform or you expand it in some kind of expansion. When you do that, you wind up with a sequence of numbers. You put the sequence of numbers into a quantizer, and the quantizer reduces that to a discrete alphabet. You put the discrete symbols into the discrete encoder. You pass it through a reliable binary channel.
What is a reliable binary channel? It's a layered view of any old channel in the world, OK? In other words, the way that discrete channels work these days is that, in almost all cases, what goes into them is a binary stream of signals, and what comes out of them is a binary stream of symbols, and the output is essentially the same z-input. That's the whole purpose of how you design digital channels, and they work over analog media and all sorts of things.
OK, so discrete encoders and discrete decoders are really a valid topic to study in their own. I mean, you have text and stuff like that, which is discrete to start with, so there's a general topic of how do you encode discrete things? We've pretty much answered that problem, at least in an abstract sense, and the main point there is you find the entropy of that discrete sequence, the entropy per symbol, and then you find ways of encoding that discrete source in such a way that the number of bits per symbol is approximately equal to that entropy. We know you can't do any better than that. You can't do an encoding, which is uniquely decodable, which you can get out of with the original symbols again, with anything less than the entropy.
So at least we know roughly what the answer to that is. We even know some classy schemes like the Lempel-Ziv algorithm, which will in fact operate without even knowing anything about what the probabilities are. So we sort of understand this block here at this point. And we could start with this next, or we could start with this next, and unlike the electrician here, we're going to move in sequence and look at this next and this third.
There's another reason for that. When we get into this question, we will be talking about what do you do with waveforms? How do you deal with waveforms? It's what you've been studying probably since the sixth grade, and you're all familiar with it. You do integration and things like that. You know how to work with functions.
What we're going to do with functions in this course is a little bit different than what you're used to. It's quite a bit different than what you learned in your Signals and Systems course, and you'll find out why as we move along.
But we have to understand this business of how to deal with waveforms, both in terms of this block, which is the final block we'll study in source coding, and also in terms of how to deal with channels because in real channels, generally what you transmit is a waveform. What the noise does to you is to add a waveform or, in some sense, multiply what you put in by something else. And all of that is waveform stuff. And all of information theory and all of digital communication is based on thinking bits. So somehow or other, we have to become very facile in going from waveforms to bits.
Now I've been around the professional communities of both communication and information theory for a long, long time. There is one fundamental problem that gives everyone problems because information theory texts do not deal with it and communication texts do not deal with it. And that problem is how do you go from one to the other, which seems like it ought to be an easy thing. It's not as easy as it looks, and therefore, we're going to spent quite a bit of time on that.
In fact, I passed out lectures 6 and 7 today, which in previous years I've done in two separate lectures because quantization is a problem that looks important. We'll see that it's not quite as important as it looks. And I guess the other thing is, I mean, at different times you have to teach different things or you get stale on it. And I've just finished writing some fairly nice notes, I think, on this question of how do you go from waveforms to numbers and how do you go from numbers to waveforms. And I want to spend a little more time on that this year than I did last year. I want to spend, therefore, a little less time on quantization, so that next time, we will briefly review what we've done today on quantization, but we will essentially just compress those two lectures all into one.
In dealing with waveforms, we're going to learn some interesting and kind of cool things. Like for those of you who really don't -- are not interested in mathematics, you know that people study things like the theory of real variables and functional analysis and all of these neat things, which are very, in a sense, advanced mathematics.
They're all based on measure theory, and you're going to find out a little bit about measure theory here. Not an awful lot, but just enough to know why one has to deal with those questions because the major results in dealing with waveforms and samples really can't be stated in any other form than in a somewhat measure-theoretic form. So we're going to find just enough about that so we can understand what those issues are about. So that's why next time we're going to start dealing with the waveform issues.
OK, so today, we're dealing with these quantizer issues and how do you take a sequence of numbers, turn them into a sequence of symbols at the other end? How do you take a sequence of symbols, turn them back into numbers?
So when you convert real numbers to binary strings, you need a mapping from the set of real numbers to a discrete alphabet. And we're typically going to have a mapping from the set of real numbers into a finite discrete alphabet. Now what's the first obvious thing that you notice when you have a mapping that goes from an infinite set of things into a finite set of things?
AUDIENCE: [INAUDIBLE]
PROFESSOR: What?
AUDIENCE: [INAUDIBLE]
PROFESSOR: Not really. It's a much simpler idea than that. How are you going to get back? I mean, usually when you map something into something else, you would like to get back again. When you map an infinite set into a finite set, how are you going to get back?
AUDIENCE: You're not.
PROFESSOR: You're not. Good! There's not any way in hell that you're ever going to get back, OK? So, in other words, what you've done here is to deliberately introduce some distortion into the picture. You've introduced distortion because you have no choice. If you want to turn numbers into bits, you can't get back to the exact numbers again. So you can only get back to some approximation of what the numbers are.
But anyway, this process of doing this is called scalar quantization, if we're mapping from the set of real numbers to a discrete alphabet. If instead you want to convert real n-tuples into sequences of discrete symbols, in other words, into a finite alphabet, you call that vector quantization because you can view n real numbers, a sequence of n real numbers as a vector within coordinates and within components. And I'm not doing anything fancy with vectors here. You just look at an n-tuple of numbers as a vector.
OK, so scalar quantization is going to encode each term of the source sequence separately. And vector quantization is first going to segment this sequence of numbers into blocks of n numbers each, and then it's going to find a way of encoding those n-blocks into discrete symbols. Does this sound a little bit like what we've already done in dealing with discrete sources? Yeah, it's exactly the same thing.
I mean, we started out by mapping individual symbols into bit sequences, and then we said, gee, we can also map n-blocks of those symbols into bits, and we said, gee, this is the same problem again. There's nothing different, nothing new. And it's the same thing here almost except here the properties of the real numbers are important.
Why are the properties of the real numbers important? Why can't we just look at this as symbols? Well, because, since we can't do this mapping in an invertable way, you have to deal with the fact that you have distortion here. There's no other way to think about it. There is distortion. You might as well face it. If you try to cover it up, it just comes up to kick you later. So we face it right in the beginning, and that's why we deal with these things as numbers.
So let's look at a simple example of what a scalar quantizer is going to do. Basically, what we have to do is to map the line R, mainly the set of real numbers, into M different regions, which we'll call R1 up to R sub M. And in this picture here, here's R1, here's R2, here's R3, here's R4, R5 and R6, and that's all the regions we have.
You'll notice one of the things that that does is it takes an enormous set of numbers, namely all these numbers less than this, and match them all into the same symbol. So you might wind up with a fair amount of distortion there, no matter how you measure distortion. All these outliers here all get mapped into a6, and everything in the middle gets mapped somehow into these intermediate values.
But every source value now in the region R sub j, we're going to map into a representation point a sub j. So everything in R1 is going to be mapped into a1. Everything in R2 is going to get mapped into a2 and so forth. Is this a general way to map R into a set of M symbols? Is there anything else I ought to be thinking about?
Well, here, these regions here have a very special property. Namely, each region is an interval. And we might say to ourselves, well, maybe we shouldn't map points into intervals. But aside from the fact that we've chosen intervals here, this is a perfectly general way to represent a mapping from the real numbers into a discrete set of things.
Namely, when you're doing a mapping from the real numbers into a discrete set of things, there's some set of real numbers that get mapped into a1, and that by definition is called R1. There's some set of numbers which get mapped into a2. That by definition is called R2 and so forth. So aside from the fact that these intervals with these regions in this picture happen to be intervals, this is a perfectly general mapping from R into a discrete alphabet.
So since I've decided I'm going to look at scalar quantizers first, this is a completely general view of what a scalar quantizer is. You tell me how many quantization regions you want, namely how big the alphabet is that you're mapping things into, and then your only problem is how do you choose these regions and how do you choose the representation points?
OK, one new thing here: Before, we said when you have a set of symbols a1 up to a6, it doesn't matter what you call them. They're just six symbols. Here it makes a difference what you call them because here they are representing real numbers and they are representing real numbers because when you map some real number on the real line into one of these letters here, the distortion is u minus a sub j. If you're mapping u into a sub j, then you get a distortion, which is this difference here.
I haven't said yet what I am interested in as far as distortion is concerned. Am I interested in squared distortion, cubed distortion, absolute magnitude of distortion? I haven't answered that question yet. But there is a distortion here, and somehow that has to be important. We have to come to grips with what we call a distortion and somehow how big that distortion is going to be.
So our problem here is somehow to trade off between distortion and number of points. As we make the number of points bigger, we can presumably make the distortion smaller in some sense, although the distortion is always going to be very big from these really big negative numbers and from really big positive numbers. But aside from that, we just have a problem of how do you choose the regions? How do you choose the points?
OK, I've sort of forgotten about the problem that we started with. And the problem that we started with was to have a source where the source was a sequence of numbers. And when we're talking about sources, we're talking about something stochastic. We need a probability measure on these real numbers that we're encoding. If we knew what they were, there wouldn't be any need to encode them. I mean, if we knew and the receiver knew, there would be no need to encode them. The receiver would just print out what they were or store them or do whatever the receiver wants to do with them.
OK, so we're going to view the source value u with the sample value of some random variable capital U. And more generally, since we have a sequence, we're going to consider a source sequence to be U1, U2, U3 and so forth, or you could consider it a bi-infinite sequence, starting at U minus infinity and working its way up forever.
And then we're going to have some sort of model, statistical model, for this sequence of random variables. Our typical model for these is to assume that we have a memoryless source. In other words, U1, U2, U3 are independent, identically distributed, random variables. That's the model we'll use until we get smarter and start to think of something else.
OK, so now each of these source values we're going to map into some representation point a sub j. That's what defines the quantizer. And now since a sub j is a sample value of a random variable U, a sub j is going to be a sample value of some random variable V. OK, in other words, the probabilities of these different sample values is going to be determined by the set of U's that math into that a sub j.
So we have a source sequence U1, U2, blah, blah, blah. We have a representation sequence V1, V2, blah, blah, blah, which is defined by if U sub k is in R sub j, then Vk is equal to a sub j.
Point of confusion here: It's not confusing now, but it will be confusing at some point to you. When you're talking about sources, you really need two indices that you're talking about all the time. OK, one of them is how to represent different elements in time. Here we're using k as a way of keeping track of what element in time we're talking about. We're also talking about a discrete alphabet, which has a certain number of elements in it, which is completely independent of time. Namely, we've just described the quantizer as something which maps real numbers into sample values. It has nothing to do with time at all. We're going to use that same thing again and again and again, and we're using the subscript j to talk about that.
When you write out problem solutions, you are going to find that it's incredibly difficult sometimes to write sentences which distinguish about whether you're talking about one element out of an alphabet or one element out of a time sequence. And everybody has that trouble, and you read most of the literature in information theory or communication theory, and you can't sort out most of the time what people are talking about because they're doing that.
I recommend to you using an element and an alphabet to talk about this sort of thing, what a sub j is or an element and a time sequence to keep track of things at different times. It's a nice way of keeping them straight.
OK, so anyway, for a scalar quantizer, we're going to be able to just look at a single random variable U, which is a continuous-valued random variable, which takes values anywhere on the real line and maps it into a single element in this discrete alphabet, which is the set a1 up to a6 that we were talking about here.
So a scalar quantizer then is just a map of this form, OK? So the only thing we need for a scalar quantizer, we can now forget about time and talk about how do you choose the regions, how do you choose the representation points? OK, and there's a nice algorithm there. Again, one of these things, which if you were the first person to think about it, easy way to become famous. You might not stay famous, but you can get famous initially.
Anyway, we're almost always interested in the mean squared error or the mean squared distortion, MSD or MSE, which is the expected value of U minus V. U is this real-valued random variable. V is the discrete random variable into which it maps. We have the distortion between U and V, which is U minus V. We now have the expected value of that squared distortion.
Why is everybody interested in squared distortion instead of magnitude distortion or something else? In many engineering problems, you should be more interested in magnitude distortion. Sometimes you're much more interested in fourth-moment distortion or some other strange thing. Why do we always use mean squared distortion? And why do we use mean-squared everything throughout almost everything we do in communication?
I'll tell you the reason now. We'll come back and talk about it more a number of times. It's because this quantization problem that we're talking about is almost always a subproblem of this problem, where you're dealing with waveforms, where you take the waveform and you sample the waveform, where you take the waveform, and you turn the waveform into some expansion.
When you find the mean-squared distortion in a quantizer, it turns out that that maps in a beautiful way into the mean-squared distortion between waveforms. If you deal with magnitudes or with anything else in the world, all of that beauty goes away, OK? In other words, whenever you want to go from waveforms to numbers, the one thing which remains invariant, which remains nice all the way through, is this mean-square distortion, mean-square value, OK?
In other words, if you want to layer this problem into looking at this problem separately from looking at this problem, almost the only way you can do it that makes sense is to worry about mean square distortion rather than some other kind of distortion. So even though as engineers we might be interested in something else, we almost always stick to that because that's the thing that we can deal with most nicely.
I mean, as engineers, we're like the drunk who dropped his wallet on a dark street, and he's searching for it, and somebody comes along. And here he is underneath a beautiful light where he can see everything. Somebody asks him what he's looking for you, and he says he's looking for his wallet. The guy looks down and says, well, there's no wallet there. The drunk says I know. I dropped it over there, but it's dark over there. So we use mean square distortion in exactly the same sense. It isn't necessarily the problem we're interested in, but it's a problem where we can see things clearly.
So given that we're interested in the mean square distortion of a scalar quantizer, an interesting analytical problem that we can play with is for a given probability density on this real random variable, and we're assuming we have a probability density and a given alphabet size M, the problem is how do you choose these regions and how do you choose these representation points in such a way as to minimize the mean square error, OK?
So, in other words, we've taken a big sort of messy amorphous engineering problem, and we said, OK, we're going to deal with mean square error, and OK, we're going to deal with scalar quantizers, and OK, we're going to fix a number of quantization levels, so we've made all those choices to start with. We still have this interesting problem of how do you choose the right regions? How do you choose the right sample points? And that turns out to be a simple problem. I wouldn't talk about if it wasn't simple.
And we'll break it into subproblems, and the subproblems are really simple. The first subproblem is if I tell you what representation points I want to use, namely, in this picture here, I say OK, I want to use these representation points. And then I ask you, how are you going to choose the regions in an optimal way to minimize mean square error? Well, you think about that for awhile, and you think about it in a number of ways. When you think about it in just the right way, the answer becomes obvious. And the answer is, let me not think about the regions here, but let me think about a particular value that comes out of the source.
Let me think, how should I construct a rule for how to take outputs from this source and map them into some number here. So if I get some output from the source u, I say, OK, what's the distortion between u and a1? It's u minus a1. And the magnitude of that is the magnitude of u minus a1. The square of it is the square of u minus a1, and then say, OK, let me compare that with u minus a2. Let me compare it with u minus a3 and so forth. Let me choose the smallest of those things.
What's the smallest stuff for any given u? Suppose I have a u which happens to be right there, for example. What's the closest representation point? Well, a3 is obviously closer than a2. And in fact for any point in here, which is closer to a3 than it is to a2, we're going to choose a3.
Now what's the set of points which are closer to a3 than they are to a2? Well, you put a line here right between a2 and a3, OK? When you put that line right between a2 and a3, everything on this side is closer to a3 and everything on this side is closer to a2. So the answer is, in fact, simple, once you see the answer. And the answer is, given these points, we simply construct bisectors between them, namely, bisectors with -- halfway between a1 and a2, we call that b1. Halfway between a2 and a3, we call that b2, and those are the separators between the regions, OK?
In other words, what we wind up doing is we define the region R sub j, the set of things which get mapped into a sub j as the region which is bounded by bj minus 1 is the average of aj and aj minus 1, and bj is the average of aj and aj plus 1, where I've already ordered the points a sub j going from left to right, OK?
And that also tells us that the minimum mean square error regions have got to be intervals. There is no reason at all to ever pick regions which are not intervals because, as soon as you start to solve this problem for any given set of representation points, you wind up with intervals. So if you ever think of using things that are not intervals for this mean square error problem, then as soon as you look at this, you say, well, aha, that can't be the best thing to do. I will make my regions intervals. I will therefore simplify the whole problem, and I'll also improve it. And when you can both simplify things and improve them at the same time, it usually is worth doing it unless you're dealing with standards bodies or something, and then all bets are off. OK, so this one part of the problem is easy. If we know what the representation points are, we can solve the problem.
OK, we have a second problem, which is just the opposite problem. Suppose then that somebody gives you the interval regions and asks you, OK, if I give you these interval regions, how are you going to choose the representation points to minimize the mean square error? And analytically that's harder, but conceptually, it's just about as easy. And let's look at it and see if we can understand it.
Somebody gives us this region here, R sub 2, and says, OK, where should we put the point a sub 2? Well, anybody have any clues as to where you want to put it?
AUDIENCE: [INAUDIBLE]
PROFESSOR: What?
AUDIENCE: At the midpoint?
PROFESSOR: At the midpoint. It sounds like a reasonable thing, but it's not quite right.
AUDIENCE: [INAUDIBLE]
PROFESSOR: What?
AUDIENCE: [INAUDIBLE]
PROFESSOR: It depends on the probability density, yes. If you have a probability density, which is highly weighted over on -- let's see, was I talking about R2 or R3? Well, it doesn't make any difference. We'll talk about R2. If I have a probability density, which looks like this, then I want a2 to be closer to the left-hand side than to the right-hand side. I want it to be a little bit weighted towards here because that's more important in choosing the mean square error.
OK, if you didn't have any of this stuff, and I said how do I choose this to minimize the mean square error, what's your answer then? If I just have one region and I want to minimize the mean square error, what do you do?
Anybody who doesn't know should go back and study elementary probability theory because this is almost day one of elementary probability theory when you start to study what random variables are all about. And the next thing you start to look at is things like variance and second moment. And what I'm asking you here is, how do you choose a2 in order to minimize the second moment of U, whatever it is in here, minus a2? Yes?
AUDIENCE: [INAUDIBLE]
PROFESSOR: I want to take the expectation of U over the region R2. In other words, to say it more technically, I want to take the expectation of the conditional random variable U, conditional on being in R2, OK? And all of you could figure that out yourselves, if you sat down quietly and thought about it for five minutes. If you got frightened about it and started looking it up in a book or something, it would take you about two hours to do it. But if you just asked yourselves, how do I do it? You'll come up with the right answer very, very soon, OK?
So subproblem 2 says let's look at the conditional density of U in this region R sub j. I'll call the conditional density -- well, the conditional density, given that you're in this region, is, in fact, the real density divided by the probability of being in that interval, OK? So we'll call that the conditional density. And I'll let U of j be the random variable, which has this density. In other words, this isn't a random variable on the probability space that we started to deal with it. It's sort of a phony random variable. But, in fact, it's the intuitive thing that you think of, OK? In other words, if this is exactly what you were thinking of, you probably wouldn't have called this a separate random variable, OK?
So this is a random variable with this density. The expected value of U of j minus a of j quantity squared, as you all know, is sigma squared of U of j plus the expected value a U of j minus a sub j quantity squared, OK? How do you minimize this? Well, you're stuck with this. This term, you minimize it by making a sub j equal to the expected value of U of j, which is exactly what you said. Namely, you set a of j to be the conditional mean of U of j conditional on being in the center.
It's harder to say mathematically than it is to see it. But, in fact, the intuitive idea is exactly right. Namely, you condition your random variable on being in that interval, and then what you want to do is choose the mean within that interval, which is exactly the sort of thing we were thinking about here.
When I drew this curve here, if I scale it, this, in fact, is the density of u conditional on being in R sub j. And now all I'm trying to do is choose the point here, which happens to be the mean which minimizes this second moment. The second moment, in fact, is this mean square error. So, bingo! That's the second problem.
Well, how do you put the two problems together? Well, you can put it together in two ways. One of them is to say, OK, well then, clearly an optimal scalar quantizer has to satisfy both of these conditions. Namely, the endpoints of the regions have to be the midpoints of the representation points, and the representation points have to be the conditional means of the points within a region that you start with.
And then you say, OK, how do I solve that problem? Well, if you're a computer scientist, and sometimes it's good to be a computer scientist, you say, well, I don't know how to solve the problem, but generating an algorithm to solve the problem is almost trivial. I start out with some arbitrary set of representation points. That should be a capital M because that's the number of points I'm allowed to use. Then the next step in the algorithm is I choose these separation points to be b sub j is the midpoint between the a's for each of these values.
Then as soon as I get these midpoints, I have a set of intervals, and my next step is to say set a sub j is equal to the expected value of this conditional random variable U of j where R sub j is now this new interval for 1 less than or equal to j less than or equal to M minus 1. This means it's open on the left side. This means it's closed on the right side, and since it's a probability density, it doesn't make any difference what it is. I just wanted to give you an explicit rule for what to do with probability zero when you happen to wind up on that special point.
OK, and then you iterate on 2 and 3 until you get a negligible improvement. And then you ask, of course, well, if I got a negligible improvement this time, maybe I'll get a bigger improvement next time. And that, of course, is true. And you then say, well, it's possible that after I can't get any improvement anymore, I still don't have the optimal solution. And that, of course, is true also. But at least you have an algorithm which makes sense and which, each time you try it, you do a little better than you did before.
Now, this mean square error for any choice of regions and any choice of representation points is going to be nonnegative because it's an expected value of squared terms. The algorithm is nonincreasing with iterations. In other words, the algorithm is going down all the time. So you have zero down here. You have an algorithm which is marching you down toward zero. It's not going to get to zero, but it has to reach a minimum. That's a major theorem in analysis, but you don't need any major theorems in analysis to see this. You have a set of numbers, which are decreasing all the time, and they're bounded underneath. After awhile, you have to get to some point, and you don't go any further. So it has a limit.
So that's nice. So you have an algorithm which has to converge. It can't keep on going. Well, it can keep on going forever, but it keeps going on forever with smaller and smaller improvements. So eventually, you might as well stop because you're not getting anywhere.
OK, well, those conditions that we stated, the way a mathematician would say this, is these Lloyd-Max conditions are necessary but not sufficient, OK? In other words, any solution to this problem that we're looking at has to have the property that the representation points are the conditional means of the intervals and the interval boundaries are the midpoints between the representation points. But that isn't necessarily enough.
Here's a simple example of where it's not enough. Suppose you have a probability density, which is running along almost zero, jumps up to a big value, almost zero, jumps up to a big value, jumps up to a big value. This intentionally is wider than this and wider than this. In other words, there's a lot more probability over here than there is here or there is here.
And you're unlucky, and you start out somehow with points like a1 and a2, and you start out with regions like R1 -- well, yeah, you want to start out with points, a1 and a2. So you start out with a point a1, which is way over here, and a point a2, which is not too far over here. And your algorithm then says pick the midpoint b1.
Here the algorithm is particularly simple because, since we're only using two regions, all you need is one separator point. So we wind up with b1 here, which is halfway between a1 and a2. a1 happens to be right in the middle of that big interval there, and there's hardly anything else here. So a1 just stays there as the conditional mean, given that you're on this side. And a2 stays as the conditional mean, given that you're over here, which means that a2 is a little closer this big region than it is to this region, but a2 is perfectly happy there. And we go back and we iterate again. And we haven't changed b1, we haven't changed a1, we haven't changed a2, and therefore, the algorithm sticks there.
Well, that's not surprising. I mean, you know that there are many problems where you try to minimize things by differentiating or all the different tricks you have for minimizing things, and you very often find local minima. People call algorithms like this hill-climbing algorithms. They should call them valley-finding algorithms because we're sitting at someplace. We try to find a better place. So we wind up moving down into the valley further and further. Of course, if it's a real geographical area, you finally wind up at the river. You then move down the river, you wind up in the ocean and all that. But let's forgot about that. Let's just assume that there aren't rivers or anything. That we just have some arbitrary geographical area. We wind up in the bottom of a valley, and we say, OK, are we at the minimum or not?
Well, with hill climbing, you can take a pair of binoculars, and you look around to see if there's any higher peak someplace else. With valley seeking, you can't do that. We're sitting there at the bottom of the valley, and we have no idea whether there's a better valley somewhere else or not, OK? So that's the trouble with hill-climbing algorithms or valley-seeking algorithms. And that's exactly what this algorithm does.
This is called the Lloyd-Max algorithm because a guy by the name of Lloyd at Bell Labs discovered it, I think in '57. A guy by the name of Joel Max discovered it again. He was at MIT in 1960, and because all the information theorists around were at MIT at that time, they called it the Max algorithm for many years. And then somebody discovered that Lloyd had done it three years earlier. Lloyd never even published it. So it became the Lloyd-Max algorithm. And now there's somebody else who did it even earlier, I think, so we should probably take Max's name off it. But anyway, sometime when I revise the notes, I will give the whole story of that.
But I hope you see that this algorithm is no big deal anyway. It was just people fortunately looking at the question at the right time before too many other people had looked at it. And Max unfortunately looked at it. He was in a valley. He didn't see all the other people had looked at it. But he became famous. He had his moment of time and then sunk gradually into oblivion except when once in awhile we call it the Lloyd-Max algorithm. Most people call it the Lloyd algorithm, though, and I really should also.
OK, vector quantization: We talked about vector quantization a little bit. It's the idea of segmenting the source outputs before you try to do the encoding. So we ask is scalar quantization going to be the right approach? To answer that question, we want to look at quantizing two sample values jointly and drawing pictures.
Incidentally, what's the simplest way of quantizing that you can think of? And what do people who do simple things call quantizers? Ever hear of an analog-to-digital converter? That's what a quantizer is. And an analog-to-digital converter, the way that everybody does it, is scalar. So that says that either the people who implement things are very stupid, or there's something pretty good about scalar quantization. But anyway, since this is a course trying to find better ways of doing things, we ought to investigate whether it is better to use vector quantizers and what they result in.
OK, well, the first thing that we can do is look at quantizing two samples. In other words, when you want to generalize a problem to vectors, I find it better to generalize it to two vectors first and see what goes on there. And one possible approach is to use a rectangular grid of quantization regions. And as I'll show you in the next slide, that really is just a camouflaged scalar quantizer again.
So you have a two-dimensional region corresponding to two real samples. So you've got two real numbers, U1 and U2. You're trying to map them into a finite set of sample values of representation points. Since you're going to be interested in the distortion between U1 and U2, between the vector U1, U2, and your representation vector, a1, a2, these points, these representation points, are going to be two-dimensional points also.
So if you start out by saying let's put these points on a rectangular grid, well, we can then look at it, and we say, well, given the points, how do we choose the regions? You see, it's exactly the same problem that you solved before. If I give you the points and then I ask you, well, if we get a vector U1, U2 that's there, what do we map it to? Well, we map it to the closest thing, which means if we want to find these regions, we set up these perpendicular bisectors halfway between the representation points.
So all of this is looking very rectangular now because we started out with these points rectangular. These lines are rectangular, and now I say, well, is this really any different from a scalar quantizer? And, of course, it isn't because for this particular vector quantizer, I can first ask the question, OK, here's U1, which is something in this direction. How do I find regions for that? Well, for U1, I just establish these regions here. And then I say, OK, let's look at U2 next. And then I look at things in this direction, and I wind up in saying, OK, that's all there is to the problem. I have a scalar quantizer again. Everything that I said before works.
Now if you're a theoretician, you go one step further, and you say, what this tells me is that vector quantizers cannot be any worse than scalar quantizers. Because, in fact, a vector quantizer has a -- or at least a vector quantizer in two dimensions -- has a scalar quantizer -- has two scalar quantizers as a special case. And therefore, the amount of square distortion that I wind up with in the vector case, I can always get that -- whatever I can do with the scalar quantizer, I can do just as well with a vector quantizer by choosing it, in fact, to be rectangular like this.
And you can also get some intuitive ideas that if instead of having IID random variables, if U1 and U2 are very heavily correlated somehow so that they're very close together, I mean, you sort of get an engineering view of what you want to do. You want to take this rectangular picture here. You want to skew it around that way. And you want to have lots of points going this way and not too many points going this way because almost everything is going this way, and there's not much going on in that direction. So you got some pictures of what you want to do.
These regions here, a little bit of terminology, are called Voronoi regions. Anytime you start out with a set of points and you put perpendicular bisectors in between those points, halfway between the points, you call the regions that you wind up with Voronoi regions. So, in fact, part of this Lloyd-Max algorithm, generalized at two dimensions, says given any set of points, the regions ought to be the Voronoi regions for them. So that's that first subproblem generalized at two dimensions.
And if you have an arbitrary set of points, the Voronoi regions look sort of like this, OK? And I've only drawn it for the center point because, well, there aren't enough points to do anything more than that. So anything in this region gets mapped into this point. Anything in this semi-infinite region gets mapped into this point and so forth. So even in two dimensions, this part of the algorithm is simple.
When you start out with the regions, with almost the same argument that we used before, you can see that the mean square error is going to be minimized by using conditional means for the representation points. I mean, that's done in detail in the notes. It's just algebra to do that. It's sort of intuitive that the same thing ought to happen, and in fact, it does.
So you can still find a local minimum by this Lloyd-Max algorithm. If you're unhappy with the fact that the Lloyd-Max algorithm doesn't always work in one dimension, be content with the fact that it's far worse in two dimensions, and it gets worse and worse as you go to higher numbers of dimensions. So it is a local minimum, but not necessarily the best thing.
OK, well, about that time, and let's go forward for maybe 10 years from 1957 and '60 when people were inventing the Lloyd-Max algorithm and where they thought that quantization was a really neat academic problem, and many people were writing theses on it and having lots of fun with it. And then eventually, they started to realize that when you try to solve that problem and find the minimum, it really is just a very ugly problem. At least it looks like a very ugly problem with everything that anybody knows after having worked on it for a very long time. So not many people work on this anymore.
So we stop and say, well, we really don't want to go too far on this because it's ugly. But then we stop and think. I mean, anytime you get stuck on a problem, you ought to stop and ask, well, am I really looking at the right problem? Now why am I or why am I not looking at the right problem? And remember where we started off. We started off with this kind of layered solution, which said we were going to quantize these things into a finite alphabet and then we were going to discrete code them, OK?
And here what we've been doing for awhile, and none of you objected. Of course, it's hard to object at 9:30 in the morning. You just listen and you -- but you should have objected. You should have said why in hell am I choosing the number of quantization levels to minimize over? What should I be minimizing over? I should be trying to find the minimum mean square error conditional on the entropy of this output alphabet. Because the entropy of the output alphabet is what determines what I can accomplish by discrete coding.
That's a slightly phony problem because I'm insisting, now at least to start with, that the quantizer is a scalar quantizer, and by using coding here, I'm allowing memory in the coding process. But it's not that phony because, in fact, this quantization job is a real mess, and this job is very, very easy. And, in fact, when you think about it a little bit, you say, OK, how do people really do this if they're trying to implement things? And how would you go about implementing something like this entire problem that we're talking about? What would you do if you had to implement it?
Well, you're probably afraid to say it, but you would use digital signal processing, wouldn't you? I mean, the first thing you would try to do is to get rid of all these analog values, and you would try to turn them into discrete values, so that you would really, after you somehow find this sequence of numbers here, you would go through a quantizer and quantize these numbers very, very finely. You would think of them as real numbers, and then you would do some kind of discrete coding, and you would wind up with something. And then you would say, ah, I have quantized these things very, very finely. And we'll see that when you quantize it very, very finely, what you're going to wind up with, which is almost optimal, is a uniform scalar quantizer, which is just what a garden-variety analog-to-digital converter does for you, OK?
But then you say, aha! What I can't do at that moment, I don't have enough bits to represent what this very fine quantizer has done. So then I think of this quantization as real numbers. I go through the same process again, and I think of then quantizing the real numbers to the number of bits I really want.
Anybody catch what I just said? I'm saying you do this in two steps. The first step is a very fine quantization, strictly for implementation purposes and for no other reason. And at that point, you have bits to process. You do digital-signal processing, but you think of those bits as representing numbers, OK? In other words, as far as your thoughts are concerned, you're not dealing with the quantization errors that occurred here at all. You're just thinking of real numbers. And at that point, you try to design conceptually what it is you want to do in this process of quantizing and discrete coding.
And you then go back to looking at these things as numbers again, and you quantize them again, and you discrete encode them again in whatever way makes sense. So you do one thing strictly for implementation purposes. You do the other thing for conceptual purposes. Then you put them together into something that works. And that's the way engineers operate all the time, I think. At least they did when I was more active doing real engineering. OK, so that's that.
But anyway, it says finding a minimum mean square error quantizer for fixed M isn't the right problem that we're interested in. If you're going to have quantization followed by discrete coding, the quantizer should minimize mean square error for fixed representation point entropy. In other words, I'd want to find these representation points. It's important what the numerical values of the representation points are for mean square error, but I'm not interested in how many of them I have. What I'm interested in is the entropy of them.
OK, so the quantizer should minimize mean square error for a fixed representation point entropy. I would like some algorithm, which goes through and changes my representation points, including perhaps changing the number of representation points as a way of reducing entropy. OK, sometimes you can get more representation points by having them out where there's virtually no probability, and therefore they don't happen very often, but when they do happen, they sure save you an awful lot of mean square error. So you can wind up with things using many, many more quantization points than you would think you would want because that's the optimal thing to do.
OK, when you're given the regions, if we try to say what happens to the Lloyd-Max algorithm then, the representation points should still be the conditional means. Why? Anybody figure out why we want to solve the problem that way? If I've already figured out what the region should the -- well, before, when I told you what the regions were, you told me that you wanted to make the representation points the conditional means. Now if I make the representation points something other than the conditional means, what's going to happen to the entropy?
The entropy stays the same. The entropy has nothing to do with what you call these symbols. I can move where they are, but they still have the same probability because they still occur whenever you wind up in that region. And therefore, the entropy doesn't change, and therefore, the same rule holds.
But now the peculiar thing is you don't want to make the representation regions Voronoi regions anymore. In other words, sometimes you want to make a region much closer to one point than to the other point. And why do you want to do that? Because you'd like to make these probabilities of the points as unequal as you can because you're trying to reduce entropy. And you can reduce entropy by making things have different probabilities.
OK, so that's where we wind up with that. I would like to say there's a nice algorithm to solve this problem. There isn't. It's an incredibly ugly problem. You might think it makes sense to use a Lagrange multiplier approach and try to minimize some linear combination of entropy and mean square error. I've never been able to make it work. So anyway, let's go on.
When we want to look at a high-rate quantizer, which is what we very often want, you can do a very simple approximation. And the simple approximation makes the problem much easier, and it gives you an added benefit. There's something called differential entropy. And differential entropy is the same as ordinary entropy, except instead of dealing with probabilities, it deals with probability densities. And you look at this, and you say, well, that's virtually the same thing, and it looks like the same thing.
And to most physicists, most physicists look at something like this, and physicists who are into statistical mechanics say, oh, of course that's the same thing. There's no fundamental difference between a differential entropy and a real entropy. And you say, well, but they're all these scaling issues there. And they say, blah, that's not important. And they're right, because once you understand it, it's not important.
But let's look and see what the similarities and what the differences are. And I'll think in terms of, in fact, a quantization problem, where I'm taking this continuous-valued random variable with density, and I'm quantizing it into a set of discrete points. And I want to say what's the difference between this differential entropy here and this discrete entropy, which we sort of understand by now.
Well, things that are the same -- the first thing that's the same is the differential entropy is still the expected value of minus the logarithm of the probability density. OK, we found that that was useful before when we were trying to understand the entropy. It's the expected value of a log pmf. Now the differential entropy is expected value of a log pdf instead of pmf.
And the entropy of two random variables, U1 and U2, if they're independent, is just the differential entropy of U1 plus the differential entropy of U2. How do I see that? You just write it down. You write down these joint densities. You write down this. The logarithm of the joint density for IID splits into a product of densities. A log of a product is the sum of the logs. It's the same as the argument before. In other words, it's not only that this is the same as the answer that we got before, but the argument is exactly the same.
And the other thing, the next thing is if you shift this density here. If I have a density, which is going along here and I shift it over to here and have a density over there, the entropy is the same again. Because this entropy is just fundamentally not -- it doesn't have to do with where you happen to be. It has to do with what these probability densities are. And you can stick that shift into here, and if you're very good at doing calculus, you can, in fact, see that when you put a shift in here, you still get the same entropy. I couldn't do that at this point, but I'm sure that all of you can. And I can do it if I spent enough time thinking it through. It would just take me longer than most of you.
OK, so all of these things are still true. There a couple of very disturbing differences, though. And the first difference is that h of U is not scale invariant. And, in fact, if it were scale invariant, it would be totally useless. The fact that it's not scale invariant turns out to be very important when you try to understand it, OK? In other words, if you stretch this probability density by some quantity a, then your probability density, which looks like this, shifts like this. It shifts down and it shifts out. So the log of the pmf gets bigger. The pmf itself is just sort of spread out. It does what you would expect it to do, and that works very nicely. But the log of the pmf has this extra term which comes in here, which is a factor of a. And it turns out you can just factor that factor of a out, and you wind up with the differential entropy of a scaled random variable U is equal to the differential entropy of the original U plus log of a, which might be minus log of a. I'm not sure which it is. I'll write down plus or minus log of a. It's one or the other. I don't care at this point. All I'm interested in is that you recognize that it's different.
An even more disturbing point is this differential entropy can be negative. It can be negative or positive. It can do whatever it wants to do. And so we're left with a sort of a peculiar thing. But we say, well, all right, that's the way it is. The physicists had to deal with that for many, many years. And the physicists, who think about it all the time, deal with it and say it's not very important. So we'll say, OK, we'll go along with this unless asked: What happens if we try to build a uniform high-rate scalar quantizer, which is exactly what you would do for implementation purposes anyway.
So how does this work? You pick a little tiny delta. You have all these regions here. And by uniform, I mean you make all the regions the same. I mean, conceptually, this might mean having accountably infinite number of regions. Let's not worry about that for the time being. And you have points in here, which are the conditional means of the regions.
Well, if I assume that delta is small, then the probability density of u is almost constant within a region, if it really is a density. And I can define an average value of f of u within each region in the following way. It's easier to see what it is graphically if I have a density here, which runs along like this. And within each region, I will choose f-bar of u to be a piecewise constant version of this density, which might be like that, OK?
Now that's just analytical stuff to make things come out right. If you read the notes about how to do this, you find out that this quantity is important analytically to trace through what's going on. I think for the level that we're at now, it's fine to just say, OK, this is the same as this, if we make the quantization very small. I mean, at some point in this argument, you want to go through and say, OK, what do I mean by approximate? Is the approximation close? How does the approximation become better as I make delta smaller, and all of these questions. But let's just now say, OK, this is the same as that, and I'd like to find out how well this uniform high-rate scalar quantizer does.
So my high-rate approximation is that this average density is the same as the true density and for all possible u. So conditional on u and Rj, this quantity is constant. It's constant and equal to 1 over delta, and the actual density is approximately equal to 1 over delta. What's that mean? It means that the mean square error in one of these quantization regions is our usual delta squared over 12, which is the mean square error of a uniform density in a region from minus delta over 2 to plus delta over 2. So that's the mean square error. You can't do anything with that. You're stuck with it.
The next question is what is the entropy as a quantizer output? I'm sorry, I'm giving a typical MIT lecture today, which people have characterized as a fire hose, and it's because I want to get done with this material today. I think if you read the notes afterwards, you've got a pretty good picture of what's going on. We are not going to have an enormous number of problems on this. It's not something we're stressing so I want to get you to have some idea of what this is all about.
This slide is probably the most important slide because it tells you what this differential entropy really is. OK, I'm going to look at the probabilities of each of these discrete points now. p sub j is the probability that the quantizer will get the point a sub j. In other words, it is the probability of the region R sub j. And that's just the integral of the probability density over the j-th region. Namely, it's the probability of being in that j-th region. p sub j is also equal to this average value times delta.
OK, so I look at what the entropy is of the high-rate quantizer. It's the sum of minus pj log pj. I translate that pj is equal to this, so I have a sum over j. I have an integral minus a fU of u, which is that, times log And now I'll use this quantity instead of this quantity. f-bar of u times delta du. OK, in other words, these probabilities are scaled by delta, which is what I was telling you before. That's the crucial thing here. As you make delta smaller and smaller, the probabilities of the intervals go down with delta.
OK, so I break this up into two terms now. I take out the log of delta, which is integrated over fU. I have this quantity left. This quantity is approximately equal to the density, and what I wind up with is that the actual entropy of the quantized version is equal to the differential entropy minus the log of delta at high rate.
OK, that's the only way I know to interpret differential entropy that makes any sense, OK, in other words, usually when you think of integrals, you think of them in a Riemann sense. You think of breaking up the interval into lots of very thin slices with delta, and then you integrate things by adding up things, and that integral then is then a sum. It's the same as this kind of sum. And the integral that you wind up with when you're dealing with a log of the pmf, you get this extra delta sticking in there, OK?
So this entropy is this phony thing minus log of delta. As I quantize more and more finely, this entropy keeps going up. It goes up because when delta is very, very small, minus log delta is a large number. So as delta gets smaller and smaller, this entropy heads off towards infinity. And in fact, you would expect that because if you take a real number, which has a distribution which is -- well, anything just between minus 1 and plus 1, for example, and I want to represent it very, very well if it's uniformly distributed there, the better I try to represent it, the more bits it takes.
That's what this is saying. This thing is changing as I try to represent things better and better. This quantity here is just some funny thing that deals with the shape of the probability density and nothing else. It essentially has a scale factor built into it because the probability density has a scale factor built into it. A probability density is probability per unit length. And therefore, this kind of entropy has to have that unit length coming in here somehow, and that's the way it comes in. That's the way it is.
So to summarize all of that, and I'm sure you haven't quite understood all of it, but if you do efficient discrete coding at the end of the whole thing, the number of bits per sample, namely, per number coming into the quantizer that you need, is H of V, OK? With this uniform quantizer, which produces an entropy of the symbols H of V, then you L-bar bits per symbol to represent that. That's the result that we had before.
This quantity H of V depends only on delta and h of U. Namely, h of U is equal to H of V plus log delta. So, in other words, analytically, the only thing you have to worry about is what is this differential entropy? You can't interpret what it is, but you can calculate it. And once you calculate it, this tells you what this entropy is for every choice of delta so long as delta is small.
It says that when you get to the point where delta is small and the probability density is essentially constant over a region, if I want to make delta half as big as it was before, then I'm going to wind up with twice as many quantization regions. They're all going to be only half as probable as the ones before. It's going to take me one extra bit to represent that, OK?
Namely, this one extra bit for each of these old regions is going to tell me whether I'm on the right side or the left side of that old quantization region to talk about the new quantization region. So this all make sense, OK? Namely, the only thing that's happening as you make the quantization finer and finer is that you have these extra bits coming in, which are sort of telling you what the fine structure is. And little h of U already has built into it the overall shape of the thing.
OK, now I've added one thing more here, which I haven't talked about at all. This uniform scalar quantizer in fact becomes optimal as delta become small. And that's not obvious; it's not intuitive. There's an argument in the text that shows why that is true. It uses a Lagrange multiplier to do it. I guess there's a certain elegance to it. I mean, after years of thinking about it, I would say, yeah, it's pretty likely that it's true if I didn't have the mathematics to know it's true. But, in fact, it's a very interesting result. It says that what you do with classical a to z converters, if you're going to have very fine quantization, is, in fact, the right thing to do.
Free Downloads
Video
- iTunes U (MP4 - 174MB)
- Internet Archive (MP4 - 174MB)
Free Streaming
Subtitle
- English - US (SRT)