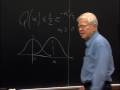Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics covered: Theorem of irrelevance, M-ary detection, and coding
Instructors: Prof. Robert Gallager, Prof. Lizhong Zheng

Lecture 18: Theory of Irrel...
SPEAKER: The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation, or to view additional material from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.
PROFESSOR: OK I want to review a little bit what we said about detection at the end of last hour, last hour and a half, because we were going through it relatively quickly. Detection is a very funny subject. Particularly the way that we do it here because we go through a bunch of very, very simple steps. Everything looks trivial-- I hope it looks trivial-- as we go, at least after you think about it for awhile, and you work with it for awhile, you will come back and look at it and you will say, "yes, in fact that is trivial." Nothing when you look at it for the first time is trivial.
And the kind of detection problems that we're interested in is-- to start out with-- we want to look just at binary detection. We're sending a binary signal, it's going to go through some signal encoder, which is the kind of channel encoder we've been thinking about. It's going to go through a baseband modulator, a baseband to passband modulator. It's going to have white Gaussian noise, or some kind of noise, added to it. It's going to come out the other end. We come back from passband to baseband. We then go through a baseband demodulator. We then sample at that point. And, the point is, when you're all done with all of that, what you've done is you've started out sending either plus a or minus a as a one- dimensional numerical signal. And when you're all through, there's some one- dimensional number that comes out, v. And on the basis of that one- dimensional number, v, you're supposed to guess whether the output is zero or one.
Now, one of the things that we're doing right now is we're simplifying the problem in the sense that we're not looking at a sequence of inputs coming in, and we're not looking at a sequence of outputs coming out. We're only looking at a single input coming in. In other words, you build this piece of communication equipment, you get it all tuned up, you get it into steady state. You send one bit. You receive something. You try to guess at the receiver, what was sent. And at that point you tear the whole thing down and you wait a year until you've set it up perfectly again. You send another bit. And we're not going to worry at all about what happens with the sequence, we're only going to worry about this one shot problem.
You sort of have some kind of clue that if you send the whole sequence of bits, in a system like this, and you don't have intersymbol interference, and the noise is white, so it's sort of independent from time to time. You sort of have a clue that you're going to get the same answer whether you send the sequence of data or whether you just send a single bit. And we're going to show later that that, in fact, is true. But for the time being we want to understand what's going on, and to understand what's going on we take this simplest possible case where there's only one bit that's being transmitted.
It's the question, "Are we going to destroy ourselves in the next five years or not?" And this question is important to most of us, and at the output we find out, in fact, whether we're going to destroy ourselves or not. So it's one bit, but it's one important bit.
OK, why are we doing things this way? Want to tell you a little story about the first time I really talked to Claude Shannon. I was a young member of the faculty at that time, and I was working on a problem which I thought was really a neat problem. It was interesting theoretically. It was important practically. And I thought, "gee, I finally have something I can go to this great man and talk to him about." So I screwed up my courage for about two days. Finally I saw his door open and him sitting there, so I went in and started to tell him about this problem.
He's a very kind person and he listened very patiently. And after about 15 minutes he said, "My god! I'm just sort of lost with all of this. There's so much stuff going on in this problem. Can't we simplify it a little bit by throwing out this kind of practical constraint you've put on it?" I said, "yeah, I guess so." So we threw that out and the we went on for awhile later, and then he said, "My god, I'm still terribly confused about this whole thing. Why don't we simplify it in some other way?"
And this went on for about an hour. As I say, he was a very patient guy. And at the end of an hour I was getting really depressed. Because here was this beautiful problem that I thought was going to make me famous, give me tenure, do all these neat things. And here he'd reduced the thing to a totally trivial toy problem. And we looked at it. And we said, yes this is a trivial toy problem. This is the answer. The problem is solved. But so what? And then he suggested putting some of those constraints back in again.
And as we started putting the constraints back in, one- by- one, we saw that each time we put a new constraint in-- since we understood the problem and its simplest form-- putting the constraint in, it was still simple. And by the time we built the whole thing back up again, it was clear what the answer was. OK, in other words, what theory means is really solving these toy problems. And solving the toy problems first. And in terms of practice, some people think the most practical thing is to be practical. And the whole point of this course, and this particular subject of detection is a wonderful example of this, the most practical thing is to be theoretical. I mean, you need to add practice to the theory, but the way you do things is you start with a theory-- which means you start with the toy problems, you build up from those toy problems, and after you build up for awhile, understanding what the practical problem is also-- you then understand how to deal with the practical problem.
And the practical engineer who doesn't have any of that fundamental knowledge about how to deal with these problems is always submerged in a sea of complexity. Always doing simulations of something that he doesn't, he or she doesn't understand. Always trying to interpret something from it, but with just too many things going on to have any idea of what it really means.
Ok, so that's why we're making this trivial assumption here. We're only putting one bit in. We're ignoring what happens all the way through the system. We only get one number out. We're going to assume that this one number here is either plus or minus a, plus the Gaussian random noise variable. And we're not quite sure why it's going to be plus or minus a, plus a Gaussian noise random variable, but we're going to assume that for the time being. OK?
So the detector observes the sample values of the random variable for which this is the sample value, and then guesses what the value of this random variable, h, which is what we call the input now. Because we view it from the standpoint of the detector-- the detector has two possible hypotheses-- one is that a zero was sent, and the other that a one was sent. And on the basis of this observation, you take first the hypothesis zero and you say, "Is this a reasonable hypothesis?" Then you look at the hypothesis one, say, "Is this a reasonable hypothesis?" And then you guess whether you think zero was more likely or one is more likely, given this observation that you've had.
So what they detector has, at this point, is a full statistical characterization of the entire problem. Mainly you have a model of the problem. You understand every probability in the universe that might have any effect on this. And what might have any effect on this-- as far as the way we've set up the problem-- is only the question of what are the probabilities that you're going to send one or the other of these signals here? And conditional on each of these, what are the probabilities of this random variable appearing at the output? Because you have to base your decision only on this. So all of the probabilities only give you this one simple thing. Hypothesis testing, decision making, decoding, all mean the same thing. They mean exactly the same thing. And they're just done by different people.
OK, so what that says is we're assuming the detector uses a known probability model. And in designing the detector, you know what that probability model is. It might not be the right probability model, and one of the things that many people interested in detection study is the question of when you think the probability model is one thing and it's actually something else, how well does the detection work? It's a little like the Lempel-Ziv algorithm that we studied earlier for doing source coding. Which is, how do you do source coding when you don't know what the probabilities are? And we found the best way to study that, of course, was to first find out how to do source encoding when you did know what the probabilities were. So we're doing the same thing here.
We assume the detector is designed to maximize the probability of guessing correctly. In other words, it's trying to minimize the probability of error. We call that a MAP detector-- maximum a posteriori probability decoding. You can try to do other things. You can say that there's a cost of one kind of error, and there's another cost of another kind of error. I mean, if you're doing medical testing or something. If you guess wrong in one way, you tell the patient there's nothing wrong with them, the patient goes out, drops dead the next day. And you don't care about that, of course, but you care about the fact that the patient is going to sue the hospital for 100 million dollars and you're going to lose your job because of it. So there's a big cost to guessing wrong in that way. But for now, we're not going to bother about the costs.
One of the things that you'll see when we get all done is that putting in cost doesn't make the problem any harder, really. You really wind up with the same kind of problem. OK, so h is the random variable that will be detected, and v is the random variable that's going to be observed. The experiment is performed. Some sample value of v is observed, and some sample value of the hypothesis has actually happened. In other words, what has happened is you prepared the whole system. Then at the input end to the whole system, the input to the channel, somebody has chosen a one or a zero without the knowledge of the receiver. That one or zero has been sent through this whole system, the receiver has observed some output, v, so in fact we're now dealing with the sample values of two different things. The sample value of the input, which is h, the sample value of the output, which is v, and in terms of the sample value of the output, we're trying to guess what the sample value of the input is.
OK, an error then occurs if, after the output chooses a particular hypothesis as its guess, and that hypothesis, then, is a function of what it receives. In other words, after you receive something, what the detector has to do is somehow map what gets received, which is some number, into either zero or one. It's like what a Quantizer does. Mainly, it maps the whole region into two different sub- regions. Some things are mapped into zero, Some things are mapped into one. This H bar then becomes a random variable, but is a random variable that is a function of what's received. So we have one random variable, H, which is what actually happened. There's another random variable, H hat, which is what the detector guesses will happen. This is an unusual random variable, because it's not determined ahead of time. It's determined only in terms of what you decide your detection rule is going to be. This is a random variable that you have some control over. These other random variables you have no control over at all. So that's the random variable we're going to choose. And, in fact, what we're going to do is we're going to say what we want to do is this MAP decoding, maximum a posteriori probability decoding, where we're trying to minimize the probability of screwing up. And we don't care whether we make an error of one kind or make an error of the other kind.
OK, is that formulation of the problem crystal clear? Anybody have any questions about it? I mean, the easiest way to get screwed up with detection is at a certain point to be going through, studying a detection problem, and then you suddenly realize you don't understand what-- you don't understand what the whole problem is about.
OK, let's assume we do know what the problem is, then. In principle it's simple. Given a particular observed value, what we're going to do is we're going to calculate the-- what we call the a posteriori probability, the probability given that particular sample value of the observation-- we're going to calculate the probability that what went into the system is a zero and what went into the system is a one.
OK? This is the probability that j is the sample value of H, conditional on what we observed. OK, if you can calculate this quantity, it tells you if I decide that-- if I guess that H is equal to j-- this in fact tells me that this is the probability that guess is correct. And if this is the probability that guess is correct, and I want to maximize my probability of guessing correctly, what do I do? Well, what I do is my MAP rule is arg max of this probability. And "arg max" means instead of trying to maximize this instead of trying to maximize this quantity over something, what we're doing is trying to find the value of j, which maximizes this. In other words, we calculate this for each value of j, and then we picked the j for which this quantity is largest.
In other words, we maximize this but we're not interested in the maximum value of it at this point. We're interested in it later because that's the probability that we're choosing correctly. What we're interested in, for now, is what is the hypothesis that we're going to guess. OK? So this probability of being correct is going to the this probability for this maximal j. And when we average over v we get the overall probability of being correct.
There's a theorem which is stated in the notes, which is one of the more trivial theorems you can think of, which says that if you do the best thing for every sample point you, in fact, have done the best thing on average. I think that's pretty clear. If you, well I mean you can read it if you want to form a proof, but if you do the best thing all the time, then it's the overall best thing.
OK, so that's the general idea of detection. And in doing this we have to be able to calculate these probabilities, so that's the only constraint. These are probabilities, which means that this set of hypothesis is discrete. If you have an uncountable infinite number of hypotheses, at that point you're dealing with an estimation problem. Because you don't have any chance in hell of getting the right answer, exactly the right answer. And therefore you have to have some criterion for how close you are.
And that's what's important in estimation. And here what's important is really, do we guess right or don't we guess right. And we don't, we don't care. There aren't any near misses here. You either get it on the nose or you don't.
OK, so we want to study binary detection now to start off with. We want to trivialize the problem because even that problem we just stated is too hard. So we're going to trivialize it in two ways. We're going to assume that there are only two hypotheses. That it's a binary detection problem. And we're also going to assume that it's Gaussian noise. And that will make it sort of transparent what's happening.
So H takes the values zero or one. And we'll call the probabilities with which it takes those values P zero and P one. These are called a priori probabilities. In other words, these are the probabilities that the hypothesis takes to value zero or one before seeing any observation. And the probabilities after you see the observation are called a posteriori probabilities. In other words, probabilities after the observation and the probabilities before the observation.
Up until about 1950 statisticians used to argue terribly about whether it was valid to assume a priori probabilities. And as you can see by thinking about it a little bit, the problem they were facing was they couldn't separate the problem of choosing a mathematical model and analyzing it from the problem of figuring out whether the model was valid or not. And at that point people studying in that area had not gotten to the point where they could say, "Well, maybe I ought to analyze the problem for different models, and then after I understand what happens for different models I then ought to go back because I'll know what's important to find out in the real problem." But up until that time, there was just fighting among everyone. Bayes was the person who decided you really ought to assume that there's a model to start with. And he developed most of detection theory at an early time. And people used to think that Bayes was a terrible fraud. Because in fact he was using models of the problem rather than nothing.
But anyway, that's where we were. We're also going to assume that, after we get all through with modulation and demodulation, and we really want to look at a general problem here. There's one discrete random variable, H, one analog random variable, which has a probability density, v, what we want to assume is that there's a probability density that we know, which is the probability density of the observation conditional on the hypothesis. We're assuming that we know this, and we know this-- we call these things likelihoods-- and in most communication problems anyway, it's far easier to get your hand on these likelihoods than it is to get your hand the a posteriori probabilities, which you're really interested in.
So we find these likelihoods, we can find the marginal density of the observation. Which is just the weighted sum. The probability that the hypothesis is zero times a conditional probability of the observation and so forth. So we're going to assume that those densities exist. We're going to assume that we know them. And then with a great feat of probability theory, we say the a posteriori probability is equal to the a priori probability times the likelihood divided by the marginal probability of v. OK?
What was the first thing you learn in probability when you started studying random variables? It was probably this formula, which says when you have a joint density of two random variables you can write it in two ways. You can either write, "density of one times density of two conditional and one is equal to the density of two times density of one conditional in two." And then you think about it a little bit and you say, "A ha!" It doesn't matter whether the first one is the density or whether it's the probability. You can deal with it in the same way. And you get this formula, which I hope is not unusual to you.
OK, so our MAP decision rule then, our MAP decision rule, remember, is to pick the more, is to find the a posteriori probability which is most probable. Because that is the probability of being correct. So, in fact, if this probability is bigger than this probability, this is the a posteriori probability that H is equal to zero. This is the a posteriori probability that H is equal to one. So we're just going to compare those two and pick the larger. And if this one is larger than this one, we pick our choice equal zero. And if it's smaller, we pick our choice equal to one. So this is what MAP detection is. Why did I make this greater than or equal and this less than? Well, if we have densities, it doesn't often make any difference. Strangely enough, it does sometimes make a difference. Because sometimes you can have a density, and the densities are the same for both of these likelihoods. And you can find situations where it's important. But when the two probabilities are the same, the probability of being correct is the same in both cases, so it doesn't make any difference what you do when you have a quality here.
And therefore we've just made a decision. We've said, OK, what we're going to do is whenever this is equal to this, we're going to choose zero. If you prefer choosing one, be my guest. All of your MAP error probabilities will be exactly the same. Nothing will change. It just is easier to do the same thing all the time.
OK, well then we look at this formula, and we say, "Well, I can simplify this a little bit." If I take this likelihood and move it over to this side, and if I take this marginal density and move it over to this side, and if I take p zero and move it over to this side, then the marginal densities cancel out. They had nothing to do with the problem. And I wind up with a ratio of the likelihoods. And what do you think the ratio of the likelihoods is called? Somebody got the smart idea of calling that a likelihood ratio. Somehow the people in statistics were much better at generating notation than the people in communication theory who have done just an abominable job of choosing notation for things.
But anyway, they call this a likelihood ratio. And the rule then becomes: if the likelihood ratio is greater than or equal to the ratio of p1 to p0, we choose zero. And if it's less, we choose one. And we call this ratio the threshold. So in fact what this says is binary MAP tests are always threshold tests. And by a threshold test I mean finds the likelihood ratio, compare the likelihood ratio with the threshold-- the threshold in fact is this ratio of a priori probabilities-- and at that point you have actually achieved the MAP test. In other words, you have done something which actually, for real, minimizes the probability of error. Maximizes the probability of being correct.
Well because of that, this thing here, this likelihood ratio, is called a sufficient statistic. And it's called a sufficient statistic because you can do math decoding just by knowing this number. OK? In other words, it says you can you can calculate these likelihoods. You can find the ratio of them-- which is this likelihood ratio-- and after you know the likelihood ratio, you don't have to worry about these likelihoods anymore. This is the only thing relevant to the problem.
Now this doesn't seem to be a huge saving, because here we're dealing with two real numbers-- well here we've reduced it to one real number-- which is something. When we start dealing with vectors, when we start dealing with wave forms, this is really a big thing. Because what you're doing is reducing the vectors to numbers. And when you reduce accountibly infinite dimensional vector to a number, that's a big advantage. It also, in terms of the communication problems we're facing, breaks up a detector into two pieces in an interesting way. Mainly it says there are things you do with the wave form in order to calculate what this likelihood ratio is, and then after you find the likelihood ratio you just forget about what the wave form was and you deal only with that.
What we're going to find out is in this problem we were looking at here-- we're going to find out later when we look at the vector problem-- in fact this thing here is in fact the likelihood ratio if you make an observation out at this point here. In other words, right at the front end of the receiver, that's where you have all the information you can possibly have. If you calculate likelihood ratios at that point what you're going to do is to find the likelihood ratio you're going to go through all this stuff right here and wind up with that which is work which is proportional to the likelihood ratio right here.
OK, so one of the things we're doing right now is we're not looking at that problem. We're only looking at the simpler problem, assuming a one dimensional problem. But the reason we're looking at it is that later we're going to show that this is, in fact, the solution to the more general problem. Which was Shannon's idea in the first place. Of, how do you solve the trivial problem first and then see what the complicated problem is.
OK, so that's what we're trying to do, summarized here for any binary detection problem where the observation has a sample value of a random something. Namely, a random vector, a random process, a random variable, a complex variable, a complex anything. Anything whatsoever, so long as you can assign a probability density to it. You calculate the likelihood ratio, which is this ratio here, so long as you have then cities even talk about. The MAP rule is to compare this likelihood ratio with the threshold data-- which is just the ratio of the a priori probabilities-- if this is greater than or equal to that, you choose zero. Otherwise you choose one. The MAP rule, as I said before, partitions this observation space into two pieces. Into two segments. And one of those pieces gets mapped into zero. One of the pieces gets mapped into one. It's exactly like a binary quanitizer. Except the rule you use to choose the the quantization regions is different. But a quanitizer maps a space into a finite set of regions. And this detection rule does exactly the same thing. And since the beginning of information theory people have been puzzling over how to make use of the correspondence between quanitization on one hand and detection on the other hand. And there are some correspondences but they aren't all that good most of the time.
OK, so you get an error when the actual hypothesis that occurred, namely the bit that got sent was i and if the observation landed in the other subset. We know that the MAP rule minimizes the error probability. So you have a rule which you can use for all binary detection problems so long as you have the density. And if you don't have a density you can generalize it without too much trouble.
OK, so we want to look at the problem in Gaussian noise. In particular we want to look at it for 2PAM. In other words for a standard PAM system, where zero gets mapped into plus a and one gets mapped into minus a. This is often called antipodal signaling because you're sending a plus something and a minus something. They are at opposite ends of the spectrum. You push them as far away as you can, because as you push them further and further away it requires more and more energy. So you use the energy you have. You get them as far apart as you can, and you hope that's going to help you. And we'll see that it does help you.
OK, so what you receive then, we'll assume, is either plus or minus a-- depending on which hypothesis occured-- plus a Gaussian random variable. And here's where the notation of communication theorists rears its ugly head. We call the variance of this random variable n 0 over 2. I would prefer to call it sigma squared but unfortunately you can't fight city hall on something like this. And everybody talks about n 0 and n 0 over 2. And you got to get used to it. So here's where we're starting to get used to it. So that's the variance of this noise random variable.
OK, we're only going to send one binary digit, H, so this is the only, this is the sole problem we have to deal with. We've made a binary choice. Added one Gaussian random variable to it. You observe the sum, and you guess. So what are these likelihoods in this case? Well, the likelihood if H is equal zero, in other words if you're sending a plus a, the likelihood is just a Gaussian density shifted over by a. And if you're sending, on the other hand, a one-- which means you're sending minus a-- you have a Gaussian density shifted over the other way. Let me show you a picture of that.
We'll come back to analyze more things about the picture in a little bit, so don't worry about most of the picture at this point. OK, this is the likelihood probability density of the output given that you sent a zero. Mainly that you sent plus a. So we have a Gaussian density-- this bell shaped curve-- centered around plus a. If you sent a one, you're sending minus a-- one gets mapped into minus a-- and you have the same bell shaped curve centered around minus a. If you receive any particular value of v, mainly suppose you receive the value of v here, you calculate these two likelihoods. One of them is this. One of them is that. You compare them, the ratio with the threshold, and you make your choice.
OK, so let's go back to do it. To do the arithmetic. Here are the two likelihoods. You take the ratio of these two things. When you take the ratio of them, what happens? And this sort of always happens in these Gaussian problems. These terms cancel out. Well it always happens in these additive Gaussian problems. These terms cancel out. You take a ratio of two exponents. You just get the difference. So the likelihood ratio-- this divided by this-- is then e to the minus v minus a squared over n0. and v plus a squared over n0. OK? Because normally the Gaussian density is something divided by two sigma squared, and sigma squared here is n0 over 2, so the 2's cancel out.
One nice thing about the notation anyway, you get rid of one factor of two in it. Well so you have this minus this. When you take the difference of these two things the v squareds cancel out. Because one of these things is in the numerator, the other one was in the denominator. So you have this term comes through as is. This is-- you're dividing by this-- so when you multiply this turns into a plus sign. So the v squared here cancels out with the v squared here. The a squared here cancels out with the a squared here. And it's only the inner product term that survives this whole thing. And here you have plus 2va. Here you have plus 2va. So you wind up with e to the 4av divided by n0. Which is very nice, because what it says is this likelihood, which is what determines everything in the world, is just a scalar in multiple of the observation. And that that's going to simplify things a fair amount. It's why that picture comes out as simply is it does.
OK, so to do a little more of the arithmetic. This is the likelihood here, e to the 4av over n0. So our rule is you compare this likelihood to the threshold-- which is p1 over p0, which we call eta-- and you look at that for awhile and you say, "Gee, this is going to be much easier to deal with. Instead of looking at the likelihood ratio, I look at the log likelihood ratio."
And people who deal with Gaussian problems a lot, you never hear them talk about likelihood ratios, you always hear them talk about log likelihood ratios. And you can find one from the other, so either one is equally good. In other words, the log likelihood ratio is a sufficient statistic, because you can calculate the likelihood ratio from it. So this is a sufficient statistic. It's equal to 4av over n0. And when this is greater than or equal the log of the threshold, you go this way. When it's less than, you go this way. So when you then multiply by n0 over 4a, your decision rule is you just look at the observation. You compare it with n0 times log of eta divided by 4a. And at this point we can go back to this picture and sort of sort out what all of it means. Because this point here is now the threshold. It's n0 times log of eta divided 4eta. By 4a. That's what we said the threshold had to be.
So we have these two Gaussian curves now. Why do we have to go back and look at these Gaussian curves? I told you that once we calculated the likelihood ratio we could forget about the curves. So why do I want to put the curves back in? Well because I want to calculate the probability of error at this point. OK?
And it's easier to calculate the probability of error if, in fact, I draw curve for myself and I look at what's going on. So here's the threshold. Here's the density when H equals one is the correct hypothesis. The probability of error is the probability that when I send one, the observation is going to be a random variable with this probability density and if it's a wild case, and I got an enormous value of noise, positive noise, the noise is going to push me over that threshold there and I'm going to make a mistake. So, in fact, the probability of error-- conditional on sending one-- is just this probability of that little space in there. OK? Which is the probability that I'm going to say that zero occurred when, in fact, one occurred. So that's my probability of error when one occurs. What's the probability of error when zero occurs? Well it's the same analysis. When zero occurs-- mainly when the correct hypothesis is zero-- the output, v, follows this probability density here. And I'm going to screw up if the noise carries me beyond this point here.
So you can see what the threshold is doing now. I mean, when you choose a threshold which is positive it makes it much harder to screw up when you send a minus a. It makes it much easier to screw up when you send a plus a. But you see that's what we wanted to do, because the threshold was positive in this case, because p1 was so much larger than p0. And because p1 is so much larger than p0-- p1 happens almost all the time-- and therefore you would normally almost choose p1 without looking at v. Which says you want to push it over that way a little bit.
OK, when you calculate this probability of error, it's the probability of the tail of a Gaussian random variable. So you define this tail variable, q of x, is the complimentary distribution function of a normal random variable. It's the integral from x to infinity of one over the square root of 2pi, e to the minus c squared over 2. I guess this would make better sense if this were a z-- one and-- oh, no. No, I did it right the first time. That's an x, because x is the limit in there, you see. So I'm calculating all of the probability density that's off to the right of x. And the probability of error when H is equal to one is this probability-- which looks like it's the tail on the negative side but if you think about it a little bit, since the Gaussian curve is symmetric, you can also look at it as a q function where now when you have this is equal to zero, this corresponds to changing this plus to a minus here and that's the only change. OK, so this looks a little ugly and it looks a little strange. I mean you can sort of interpret this part of it here-- I can interpret this part if I'm using maximum likelihood decoding-- maximum likelihood is mapped decoding where the threshold is equal to one. In other words, it's where you're assuming that the hypothesis is equally likely to be zero or one-- a priori-- which is a good assumption almost always in communication because we work very hard in doing source coding to make those binary digits equally likely zero or one. And there are other reasons for choosing maximum likelihood. If you don't know anything about the probabilities it's a good assumption in a sort of a max/min sense. It sort of limits how much you can screw up by having the wrong probability, so it's a very robust choice also.
OK, but now this, we're taking the ratio of a with the square root of n0. Well the square root of n0 over 2 is really the standard deviation of the noise. So what we're doing is comparing the amount of input we've put in with the standard deviation of the noise. Now does that make any sense? The probability of error depends on that ratio? Well yeah, it makes a whole lot of sense. Because if, for example, I wanted to look at this problem in a different scaling system-- if this is volts and I want to look at it in milli-volts-- I'm going to divide a by, I'm going to multiply a by 1000. I'm going to multiply the standard deviation of the noise by 1000. Because one of the things we always do here-- the way we choose n0 over 2-- n0 over 2 is sort of a meaningless quantity. It's the noise energy in one degree of freedom in the scaling reference that we're using for the data. OK? And that's the only definition you can come up with that makes any sense.
I mean you scale the data in whatever way you please, and when we've gone from baseband to passband, we in fact have multiplied the energy in the input by a factor of two. And therefore, because of that, we're going to-- n0 at passband is going to be a square root of 2 bigger than it is at baseband. If you don't like that, live with it. That's the way it is. Nobody will change n0, no matter who wants them to change it.
OK, so this term make sense. It's the ratio of the signal amplitude to the standard deviation of the noise. And that should be the only way that the signal amplitude or the standard deviation of the noise enters in, because it's really the ratio that has to be important. Why this crazy term? Well if you look at the curve you can sort of see why it is. The threshold test is comparing the likelihood ratio of this curve with the likelihood ratio of this curve. What's going to happen as a gets very, very large? You move a out, and the thing that's happening then is this curve-- which is now coming down in a modest way here-- if you move a way out here, you're going to have almost nothing there. And it's going to be going down very fast. It's going to be going down very fast relative to its magnitude. In other words the bigger a gets, the bigger this difference is going to be for any given threshold.
And that's why you get a over square root of n0 here. And here you get exactly the opposite thing. That's because for a given threshold, as this signal to noise ratio gets bigger, this threshold term becomes almost totally unimportant. I mean you get so much information out of the reading you're making, because it's so reliable, that having a threshold is almost completely irrelevant. And therefore you can sort of forget about it. If a is very large, this term is zilch. OK?
So if you want to have reliable communication and you use a large amount of single noise ratio to get it, that's another reason for forgetting about whether the threshold is one or something else. And we would certainly like to deal with problems where the threshold is equal to one because most people who remember q of a signal to noise ratio. I don't know anybody who can remember this formula. I'm sure there's some people, but I don't think anybody who works in the communication field ever thinks about this at all. Except the first time they derive it and the say, "Oh, that's very nice." And then they promptly forget about it. The only reason I think about it more is I teach the course sometimes. Otherwise I would forget about it, too.
OK, which is what this says. For communication we assume p0 is equal to p1. So we assume that eta is equal to one. So the probability of error, which is also the probability of error when H is equal to one-- in other words when a one actually enters the communication system-- is equal to the probability of error when H is equal to 0. In other words these two tails here, when the threshold is equal to one you set the threshold right there. The probability of this tail is clearly equal to the probability of this tail. Just by symmetry. So these two error probabilities are the same. And in fact they are just q of a over the square root of n0 over 2. It's nice to put this in terms of energy. We said before that energy is sort of important in the communication field. So we call e sub b the energy per bit that we're spending to send data. I mean don't worry about the fact that we're only sending one bit and then we're tearing the communication system down. Because pretty soon we're going to send multiple bits. But the amount of energy we're spending sending this one bit is a squared. At least back in this frame of reference that we're looking at now, where we're just looking at this discrete signal and single variable noise. And n0 over 2 is the noise variance of this particular random variable, z, so when we write this out in terms of Eb, which is a squared, it looks like this-- it's 2eb over n0. So the probability of error for this binary communication problem is just the square root of 2Eb over n0. Which is a formula that you want to remember. It's the error probability for binary detection when n0 over 2 is the noise energy on this one degree of freedom and Eb is the amount of energy you're spending on this one degree of freedom.
You will see about 50 variations of this as we go on. If you try to remember this fundamental definition, it'll save you a lot of agony. Even so, everybody I know who deals with this kind of thing always screws up the factors of twos. And finally when they get all done, they try to figure out from common sense or from something else, what the factors of two ought to be. And they reduce their probability of error to about a quarter after they're all done with doing all of that.
OK, so we spent a lot of time analyzing binary antipodal signals. What about the binary non antipodal signals? This is beautiful example of Shannon's idea of studying the simplest cases first. If you have two signals, one of which is b and one of which is b prime, and they can be put anywhere on the real line. And what I've done, because I didn't want to plot this whole picture again, is I just took the zero out, and I replaced the zero by the point halfway between these two points which is b plus b prime over 2. And then we look at it and we say what happens if you have an arbitrary set of two points anywhere on the real line? Well when I send this point the likelihood, conditional on this point being sent, is this Gaussian curve centered on b prime. When I send b the likelihood is a Gaussian curve centered on b. And it is in fact the same curve that we drew before. If in fact I replaced zero with a center point between these two, which is b plus b prime over 2. And if I then define a as this distance in here, the probability of error that I calculated before is the same as it was before.
Now I would suggest to all of you that you try to find the probability of error for this system here, just not using what we've already done, and just writing out the likelihood ratios as a function of an arbitrary b prime and an arbitrary b and finding a likelihood ratio, and calculating through all of that. And most of you are capable of calculating through all of it. But when you do so, you will get a god awful looking formula, which just looks totally messy. And by looking at the formula you are not going to be able to realize that what's going on is what we see here from the picture. And the only reason we figured out what was going like the picture is we already solved the problem for the Simpson case.
OK so it never makes any sense in this problem to look at this general case. You always want to say the general case is just a special case of a special case. Where you just have to define things slightly differently. OK, so we're going to do the center point, then, I mean it might be a pilot tone. It might be any other non information bearing signal. In other words were sending the one bit. Sometimes for some reason or other, you need to get synchronization. You need to get other things in a communication system. And for that reason, you send other things. We'll talk about a lot of those later. But they don't change the error probability at all. The error probability is determined solely by the distance between these two points which we call 2a.
So probability of error remains the same in terms of this distance. The energy per bit now changes. The energy per bit is the energy here plus the energy here. Which in fact is the energy in the center point plus a squared. I mean we've done that in a number of contexts, the way to find the energy in a binary random variable is to take the energy in the center point plus the energy in the difference. It's the same as finding the fluctuation plus the square of the mean. It's that same underlying idea.
So any time you use non antipodal and you shift things off the mean, you can see what's going on very, very easily. You waste energy. I mean it might not be wasted, you might have to waste it for some reason. But as far as a communication is concerned you're simply wasting it. So your energy per bit changes, but your probability of error remains the same. Because of that, you get a very clear cut idea of what it's costing you to send that pilot tone. Because in fact what you've done is to just increase this energy, which we talk about in terms of db. If c is equal to a in this case which, as will see, is a common thing that happens in a lot of systems, what you've lost is a factor three db. Because you're using twice as much energy which is three db more energy, than you have to use for the pure communication. So it's costing you three db to do whatever silly thing you want to do for synchronization or something else. Which is why people work very hard to try to send signals which carry their own synchronization information in them. And we will talk about that more when we get to wireless and things like that.
OK. Let's go on to real antipodal vectors in white Gaussian noise. And again, let me point out to you again that one of the remarkable things about detection theory is once you understand detection for antipodal binary signals and Gaussian noise, everything else just follows along. OK, so here what we're going to do is to assume that under the hypothesis H equals zero-- in other words conditional on a zero entering the communication system-- what we're going to send is not a single degree, is not something in a single degree of freedom. But we're actually going to send a vector. And you can think of that if you want to as sending a way form and breaking up the waveform into an orthonormal expansion and a1 to ak as being the coefficients in that expansion. So we're going to use several degrees of freedom to send one signal. Yes?
AUDIENCE: [INAUDIBLE]
PROFESSOR: I'm only sending one bit. And on Wednesday I'm going to talk about what happens when we want to send multiple bits or when we want to send a large number of signals in one degree of freedom, or all those cases, multiple hypotheses. You know what's going to happen? It's going to turn out to be a trivial problem again. Multiple hypotheses are no harder than just binary hypotheses. So again, once you understand the simplest case, all Gaussian problems turn out to be solved. Just with minor variations and minor tweaks.
OK, so I have antipodal vectors. One vector is a1 to a sub k. Under the other hypothesis we're going to send minus a, which is the opposite vector. So if we're dealing with two dimensional space with coordinates here and here, if I send this I'm going to send this. If I send that I'm going to send that, and so forth. As the opposite alternative. The likelihood ratio is then, the probability of vector v conditional on sending this. I'm assuming here that the noise is IID and each noise variable has mean zero and variance n0 over 2. Namely, we're pretending we're communication people here, using and n0 over 2 here.
So the conditional density-- the likelihood of this output vector given zero-- is just this density of z shifted over by a. So it's what we've talked about as the Gaussian density. Just this, which is just the energy in v minus a is what that turns out to be. So the log likelihood ratio is the ratio of this quantity to the density where H is equal to one. And when H is equal to one, what happens is the same thing as happened before. One makes this sign turn into a plus sign. So when I look at the log likelihood ratio, I want to take the ratio of this quantity to the same quantity with a plus put into it. And when I take the log of that, what happens is I get this term minus the opposite term of the opposite side. So I have minus the norm squared of v minus a plus the norm squared of v plus a over n0.
And again, if you multiply this out, the v squareds cancel out. The a squareds cancel out. And you just get the inner product terms. And strangely enough you get the same formula that you got before, almost, except here you have the inner product of v with a instead of just the product of v times a. So in fact we just have a slight generalization of the thing that we did before. In other words, the scalar product is a sufficient statistic. Now what does that tell you? It tells you how to build a detector. OK? It tells you when you have a vector detection problem, the thing that you want to do is to take this vector, v, that you have and form the inner product of v times a. If in fact v is a waveform and a is a waveform, what do you do then? Well the first thing you do is to think of v as being a vector-- where it's the vector of coefficients-- in the expansion for that waveform and a in the same way. You look at what the inner product is then, and then you say, "well what does that correspond to when I deal with L2 waveforms?" What's the inner product for L2 waveforms? It's the integral of the product of the waveforms. And how do you form the integral of the product of the waveforms? You take this waveform here. You turn it around and you call it a matched filter to a. And you take the received waveform. You pass it through the max filter for a, and you look at the output for it.
Now, let's go back and look at what all of this was doing. And for now let's forget about the baseband to the passband business. Let's just look at this part here because it's a little easier to see this first. So this comes in here. Now remember what we were saying when we studied Nyquist. We said a neat thing to do was to use a square root of the Nyquist pulse at the transmitter. When you use a square root of the Nyquist pulse at the transmitter, what you have is orthogonality between the pulse and all of its shifts. Well now we don't much care about the orthogonality between the pulse and all of the shifts because we're only sending this one bit anyway. But it sort of looks like we're going to be able to put that back in in a nice convenient way. So we're sending this one pulse, p of t, city and what did we do in this baseband demodulator? We passed this through another filter, q of t, which was the matched filter to p of t. What's our optimal detector for maximum likelihood? It's to take whatever this waveform was, pass it through the matched filter. In other words, to calculate that inner product we just talked about. OK?
So in fact when we were looking at the Nyquist problem and worrying about inner symbol interference, in fact what we were doing was also doing the first part of an optimal MAP detector. And at this point what comes out of here is a single number, v, which in fact now is the inner product of this waveform at this point. With the waveform, a, that we sent. OK? In other words, we started out by saying, "let's suppose that what we have here is a number. What's the optimal detector to build?" And then we go on and say, "OK, let's suppose we look at the problem here. What's the optimal detector to build now?" And the optimal detector to build now at this point is this matched filter to this input waveform. Followed by the inner product here-- which is what the match filter does for us-- followed by our binary antipodal detector again. OK?
So by studying the problem at this point, we now understand what happens at this point. And do I have time to show you what happens at this point? I don't know. Let me-- let's not do that at least right now-- let's look at the picture of this that we get when we just look at the problem when we have two dimensions. So we're either going to transmit a vector, a, or we're going to transmit a vector, minus a. And think of this in two dimensions. When we transmit the vector, a, we have two dimensional noise. We've already pointed out that two dimensional Gaussian noise has circular symmetry. Spherical symmetry in an arbitrary number of dimension. So what happens is you get these equal probability regions which are spreading out like when you drop a rock into a pool of water. You see all of these things spreading out in circles. And you then say, "OK, what's this inner product going to correspond to?" Finding the inner product and comparing it with a threshold.
Well you can see geometrically what's going to happen here. You're trying to do maximum likelihood. And we already know we're supposed to calculate the inner product, so what the inner product is going to do is take whatever v that we receive-- it's going to project it on to this line between 0 and a. So if I got a v here I'm going to project it down to here. And then what I'm going to do is I'm going to compare the distance from here to there with the distance from here to there. Which says first project, then do the old decision in a one dimensional way. Now geometrically, this distance squared is equal to this distance squared plus this distance squared. And this distance squared is equal to the same distance squared plus this distance squared.
So whatever you decide to do in terms of these distances, you will also decide to do in terms of these distances. Which also means that the maximum likelihood regions that you're going to develop, or in fact the maximum a posteriori probability regions are simply planes. Which are perpendicular to the line between minus a and plus a. OK? So if you're doing maximum likelihood you just form a plane halfway between these two points. Yeah?
AUDIENCE: [UNINTELLIGIBLE] PROFESSOR: We got the error probability just by first doing the projection and then turning it into this scale or problem again. So in fact the error probability-- What?
AUDIENCE: [UNINTELLIGIBLE]
PROFESSOR: The probability of error is just the probability of error in the projection. Did I write it down someplace? Oh yeah, I did write it down. But I wrote it down, well I sort of cheated. It's in the notes. I mean the likelihood ratio is just a center product here which is a number. And when you find the error probability, you just use the same q formula that we used before. And in place of a you substitute-- in place of a you substitute the inner product of v with a. Which is the corresponding quantity. So it's q of 4va divided by n0. OK?
So that's the maximum likelihood error probability. OK? In other words, nothing new has happened here. You just go through the match filter and then you do this same one dimensional problem that we've already figured out how to do.
I think I'm going to stop there and we'll do the complex case which really corresponds to what happens after baseband to passband then passband to baseband.
Free Downloads
Video
- iTunes U (MP4 - 158MB)
- Internet Archive (MP4 - 158MB)
Free Streaming
Subtitle
- English - US (SRT)