
Session Overview
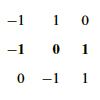 | If A is symmetric and positive definite, there is an orthogonal matrix Q for which A = QΛQT. Here Λ is the matrix of eigenvalues. Singular Value Decomposition lets us write any matrix A as a product UΣVT where U and V are orthogonal and Σ is a diagonal matrix whose non-zero entries are square roots of the eigenvalues of ATA. The columns of U and V give bases for the four fundamental subspaces. |
Session Activities
Lecture Video and Summary
- Watch the video lecture
Singular Value Decomposition (00:41:35)
Lecture 29: Singular Value Decomposition
> Download from iTunes U (MP4 - 93MB)
> Download from Internet Archive (MP4 - 93MB)
- Read the accompanying lecture summary (PDF)
- Lecture video transcript (PDF)
Suggested Reading
- Read Section 6.7 in the 4th edition or Section 7.1 and 7.2 in the 5th edition.
Problem Solving Video
- Watch the recitation video on
Computing the Singular Value Decomposition (00:11:35)
Problem Solving: Computing the Singular Value Decomposition
> Download from iTunes U (MP4 - 25MB)
> Download from Internet Archive (MP4 - 25MB)
- Recitation video transcript (PDF)
Check Yourself
Problems and Solutions
Work the problems on your own and check your answers when you're done.
