Instructor Insights pages are part of the OCW Educator initiative, which seeks to enhance the value of OCW for educators.
Course Overview
This page focuses on the course 18.783 Elliptic Curves as it was taught by Dr. Andrew Sutherland in Spring 2017.
The course is a computationally focused introduction to elliptic curves, with applications to number theory and cryptography.
A key feature of the course that distinguishes it from most other introductory courses on elliptic curves is that it provides a rigorous mathematical treatment of the subject while at the same time addressing issues of algorithmic efficiency that are crucial to practical implementations. This includes, in particular, a thorough treatment of isogenies and the theory of complex multiplication, topics that are often not covered in a first course on the subject. These concepts are crucial to many theoretical and practical applications of elliptic curves.
The latter part of the course surveys some more advanced topics, including Galois representations, modular forms, and the proof of Fermat's Last Theorem.
Some of the theorems and algorithms presented in lecture are demonstrated using the Sage computer algebra system. Most of the problem sets contain at least one computationally-focused problem.
Course Outcomes
Course Goals for Students
The goal of the course is to provide a thorough introduction to the theory of elliptic curves with a focus on computational applications. These include algorithms for factoring integers and proving primality, as well as elliptic curve cryptography.
Possibilities for Further Study/Careers
Students who complete the course should be well prepared for more advanced study and even to begin research on topics related to elliptic curves. Indeed, an unstated goal of the course is to help prepare undergraduate students for graduate school. For students in pure mathematics this may include topics in number theory and algebraic geometry (and in particular, arithmetic geometry). Students in computer science will often pursue computational applications of elliptic curves, particularly in cryptography.
Below, Dr. Andrew Sutherland describes how surveys have shaped his teaching in 18.783 Elliptic Curves.
Including Surveys at the End of Each Problem Set
I first taught this course in Spring 2012. Because it was a brand new course, I wanted to be able to adapt the material to the students as the course went along. A lot of the material is traditionally covered only in graduate courses, but I felt strongly that it could be made accessible to undergraduates if it was presented in the right way. In order to achieve this I knew it would be crucial to get feedback as I went along to make sure students weren't getting lost. I wanted to be sure I was actually getting feedback from everyone, not just those bold enough to speak up.
What I decided to do is include a survey at the end of each problem set, and students were required to submit feedback as part of the assignment. Here is a sample survey:
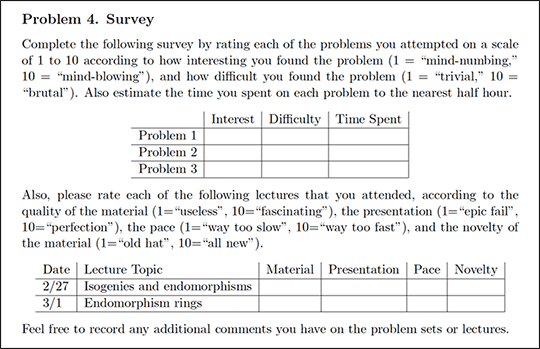
Changes to Problems Sets and Lectures Based on Survey Results
The surveys allow me to fine-tune the material, improve the course in each iteration, and respond to the students' needs and backgrounds (the mix of students varies from year to year). I actually do a post mortem on each problem set after I have graded it, reading all the surveys and taking note of specific improvements I want to make in the future. Some of the changes I have made to the problem sets in response to students' survey feedback include:
- dropping problems that received low interest ratings -- there is no reason to ask MIT students to solve routine or boring problems;
- adding more problems so that students have more freedom to choose between computational and proof-oriented problems (math students tend to prefer proofs, while computer science students tend to prefer programming);
- clarifying points of confusion, adding hints in some cases, and removing hints in others;
- adding more motivation to problems where students indicated they didn't necessarily see the connection or relevance to the course; and
- adding problems that build on material about which students expressed an interest.
In many of the cases where I dropped problems, I moved material from the problem set into the lecture notes. For example, if there is an important formula that needs to be derived but the derivation is uninteresting, it is better to put it in the lecture notes where students can see it, but are not forced to trudge through the details when they are unenlightening. I have also added material to the lectures to better address points that caused confusion on the problem sets, and in some cases to provide more motivation. Additionally, I have changed my lectures to address comments about pacing. Usually this involves covering less material in the in-class lecture in order to slow down the pace, relying on the lecture notes to fill in details omitted in the lecture. In several instances I have received requests to address some specific background topics that are not official course pre-requisites (e.g. in topology, complex analysis, and commutative algebra) in the lecture notes. I have added some quick review/primer material on some of these topics to the lecture notes for the benefit of those who have less mathematical background.
Dialogue with Students about Surveys
I respond directly to students, when appropriate, about their survey feedback. This dialogue usually takes place via e-mail. When I return their electronically marked-up problem sets, I also respond to any comments they made on the surveys, and often this will lead to some back and forth communication. One nice thing about doing this is that it gives me a chance to engage with students who don't typically attend the lectures (this is not uncommon at MIT, as there are always a few students who prefer to read the material on their own rather than coming to lecture; these students often give the best feedback on the lecture notes). Perhaps the most useful thing I have learned as an educator from this dialogue is that it is very empowering (both for them and me) when students help to shape their own education. MIT students want to optimize everything and they have little patience for poor design. This can make them harsh critics, but it also makes them enthusiastic collaborators when they feel they are partners in the process.
Advice for Educators Interested in Implementing Surveys
My advice for educators interested in implementing surveys is to demonstrate responsiveness early on, so that it is clear to students that their feedback can actually make a difference in real time. Otherwise, the surveys will just feel like an additional burden. In the internet age we get asked to respond to surveys from companies and marketing firms all the time, but in most cases these surveys do not benefit us directly. We know that our responses are probably just a drop in an ocean of data that is unlikely to trigger any short term change. When students realize their feedback might actually impact the next problem set or lecture, they become much more responsive. But in order for this to work, educators need to grade and read the survey results promptly. I usually read the survey results immediately when the problem sets are turned in and try to return the graded problem sets and the survey responses to students within 3-4 days. I have found that students like to see the results of the surveys, particularly how other students rated the difficulty and their interest level in the problems. Half the fun of participating in a poll is seeing the poll results!
Curriculum Information
Prerequisites
Corequisite
Requirements Satisfied
- H-Level graduate credit
 , except for graduate students in mathematics.
, except for graduate students in mathematics. - 18.783 can be applied toward a Bachelor of Science in Mathematics.
Offered
Every other Spring semester.
Assessment
Students’ grades were determined by their average problem set score. If they complete the weekly surveys, their lowest scores were dropped when computing the average. There were no exams and no final.
Student Information

Breakdown by Year
While 18.783 is listed as a graduate-level class, it was been taken by a mix of students consisting primarily of juniors, seniors, and graduate students.
Breakdown by Major
About 2/3 undergraduate math majors and 1/3 graduate students in computer science.
During an average week in the spring semester, students were expected to spend 12 hours on the course, roughly divided as follows:
Lecture
- Met 2 times per week for 1.5 hours per session; 26 sessions total.
- Several of the lectures included interactive sessions using Sage. The Sage worksheets are listed in the lecture notes section.
Out of Class
- There was no required textbook, but references to several books and articles were provided for each class session.
- The problem sets included both theoretical questions and practical examples that required the students to implement algorithms in Sage.
Semester Breakdown
| WEEK | M | T | W | Th | F |
|---|---|---|---|---|---|
| 1 |  |  |  |  |  |
| 2 |  |  |  |  |  |
| 3 |  |  |  |  |  |
| 4 |  |  |  |  |  |
| 5 |  |  |  |  |  |
| 6 |  |  |  |  |  |
| 7 |  |  |  |  |  |
| 8 |  |  |  |  |  |
| 9 |  |  |  |  |  |
| 10 |  |  |  |  |  |
| 11 |  |  |  |  |  |
| 12 |  |  |  |  |  |
| 13 |  |  |  |  |  |
| 14 |  |  |  |  |  |
| 15 |  |  |  |  |  |
| 16 |  |  |  |  |  |
 No classes throughout MIT
No classes throughout MIT Lecture session and office hours
Lecture session and office hours No class session scheduled
No class session scheduled Problem set due date
Problem set due date

 Room 1 of 1
Room 1 of 1 