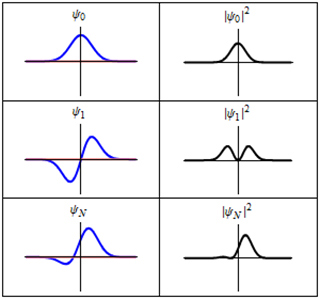
Each of these three rows is a wave function which satisfies the time-dependent Schrödinger equation for a harmonic oscillator. (This image is in the public domain. Original animated image by Sbyrnes321 on Wikipedia.)
Instructor(s)
Prof. Lawrence Guth
MIT Course Number
18.156
As Taught In
Spring 2016
Level
Graduate
Course Description
Course Features
Course Description
In this course, we study elliptic Partial Differential Equations (PDEs) with variable coefficients building up to the minimal surface equation. Then we study Fourier and harmonic analysis, emphasizing applications of Fourier analysis. We will see some applications in combinatorics / number theory, like the Gauss circle problem, but mostly focus on applications in PDE, like the Calderon-Zygmund inequality for the Laplacian, and the Strichartz inequality for the Schrodinger equation. In the last part of the course, we study solutions to the linear and the non-linear Schrodinger equation. All through the course, we work on the craft of proving estimates.
Other Versions
Other OCW Versions
OCW has published multiple versions of this subject. ![]()


