Reading 17: Regular Expressions & Grammars
Software in 6.005
| Safe from bugs | Easy to understand | Ready for change |
|---|---|---|
| Correct today and correct in the unknown future. | Communicating clearly with future programmers, including future you. | Designed to accommodate change without rewriting. |
Objectives
After today’s class, you should:
- Understand the ideas of grammar productions and regular expression operators
- Be able to read a grammar or regular expression and determine whether it matches a sequence of characters
- Be able to write a grammar or regular expression to match a set of character sequences and parse them into a data structure
Introduction
Today’s reading introduces several ideas:
- grammars, with productions, nonterminals, terminals, and operators
- regular expressions
- parser generators
Some program modules take input or produce output in the form of a sequence of bytes or a sequence of characters, which is called a string when it’s simply stored in memory, or a stream when it flows into or out of a module. In today’s reading, we talk about how to write a specification for such a sequence. Concretely, a sequence of bytes or characters might be:
- A file on disk, in which case the specification is called the file format
- Messages sent over a network, in which case the specification is a wire protocol
- A command typed by the user on the console, in which case the specification is a command line interface
- A string stored in memory
For these kinds of sequences, we introduce the notion of a grammar , which allows us not only to distinguish between legal and illegal sequences, but also to parse a sequence into a data structure that a program can work with. The data structure produced from a grammar will often be a recursive data type like we talked about in the recursive data type reading .
We also talk about a specialized form of a grammar called a regular expression . In addition to being used for specification and parsing, regular expressions are a widely-used tool for many string-processing tasks that need to disassemble a string, extract information from it, or transform it.
The next reading will talk about parser generators, a kind of tool that translate a grammar automatically into a parser for that grammar.
Grammars
To describe a sequence of symbols, whether they are bytes, characters, or some other kind of symbol drawn from a fixed set, we use a compact representation called a grammar .
A grammar defines a set of sentences, where each sentence is a sequence of symbols. For example, our grammar for URLs will specify the set of sentences that are legal URLs in the HTTP protocol.
The symbols in a sentence are called
terminals
(or tokens).
They’re called terminals because they are the leaves of a tree that represents the structure of the sentence.
They don’t have any children, and can’t be expanded any further.
We generally write terminals in quotes, like
'http'
or
':'
.
A grammar is described by a set of productions , where each production defines a nonterminal . You can think of a nonterminal like a variable that stands for a set of sentences, and the production as the definition of that variable in terms of other variables (nonterminals), operators, and constants (terminals). Nonterminals are internal nodes of the tree representing a sentence.
A production in a grammar has the form
nonterminal ::= expression of terminals, nonterminals, and operators
In 6.005, we will name nonterminals using lowercase identifiers, like
x
or
y
or
url
.
One of the nonterminals of the grammar is designated as the
root
.
The set of sentences that the grammar recognizes are the ones that match the root nonterminal.
This nonterminal is often called
root
or
start
, but in the grammars below we will typically choose more memorable names like
url
,
html
, and
markdown
.
Grammar Operators
The three most important operators in a production expression are:
- concatenation
x ::= y z an x is a y followed by a z - repetition
x ::= y* an x is zero or more y - union (also called alternation)
x ::= y | z an x is a y or a z You can also use additional operators which are just syntactic sugar (i.e., they’re equivalent to combinations of the big three operators):
- option (0 or 1 occurrence)
x ::= y? an x is a y or is the empty sentence- 1+ repetition (1 or more occurrences)
x ::= y+ an x is one or more y
(equivalent to x ::= y y* )- character classes
x ::= [abc] is equivalent to x ::= 'a' | 'b' | 'c'
x ::= [^b] is equivalent to x ::= 'a' | 'c' | 'd' | 'e' | 'f'
| ... (all other characters)
By convention, the operators
*
,
?
, and
+
have highest precedence, which means they are applied first. Alternation
|
has lowest precedence, which means it is applied last. Parentheses can be used to override this precedence, so that a sequence or alternation can be repeated:
- grouping using parentheses
x ::= (y z | a b)* an x is zero or more y-z or a-b pairsExample: URL
Suppose we want to write a grammar that represents URLs. Let’s build up a grammar gradually by starting with simple examples and extending the grammar as we go.
Here’s a simple URL:
http://mit.edu/A grammar that represents the set of sentences containing only this URL would look like:
url ::= 'http://mit.edu/'But let’s generalize it to capture other domains, as well:
http://stanford.edu/
http://google.com/We can write this as one line, like this:

url ::= 'http://' [a-z]+ '.' [a-z]+ '/'
This grammar represents the set of all URLs that consist of just a two-part hostname, where each part of the hostname consists of 1 or more letters. So
http://mit.edu/
and
http://yahoo.com/
would match, but not
http://ou812.com/
. Since it has only one nonterminal, a
parse tree
for this URL grammar would look like the picture on the right.
In this one-line form, with a single nonterminal whose production uses only operators and terminals, a grammar is called a regular expression (more about that later). But it will be easier to understand if we name the parts using new nonterminals:

url ::= 'http://' hostname '/'
hostname ::= word '.' word
word ::= [a-z]+
The parse tree for this grammar is now shown at right. The tree has more structure now. The leaves of the tree are the parts of the string that have been parsed. If we concatenated the leaves together, we would recover the original string. The
hostname
and
word
nonterminals are labeling nodes of the tree whose subtrees match those rules in the grammar. Notice that the immediate children of a nonterminal node like
hostname
follow the pattern of the
hostname
rule,
word '.' word
.
How else do we need to generalize? Hostnames can have more than two components, and there can be an optional port number:
http://didit.csail.mit.edu:4949/To handle this kind of string, the grammar is now:

url ::= 'http://' hostname (':' port)? '/'
hostname ::= word '.' hostname | word '.' word
port ::= [0-9]+
word ::= [a-z]+Notice how hostname is now defined recursively in terms of itself. Which part of the hostname definition is the base case, and which part is the recursive step? What kinds of hostnames are allowed?
Using the repetition operator, we could also write hostname like this:
hostname ::= (word '.')+ wordAnother thing to observe is that this grammar allows port numbers that are not technically legal, since port numbers can only range from 0 to 65535. We could write a more complex definition of port that would allow only these integers, but that’s not typically done in a grammar. Instead, the constraint 0 <= port <= 65535 would be specified alongside the grammar.
There are more things we should do to go farther:
-
generalizing
httpto support the additional protocols that URLs can have -
generalizing the
/at the end to a slash-separated path - allowing hostnames with the full set of legal characters instead of just a-z
Example: Markdown and HTML
Now let’s look at grammars for some file formats. We’ll be using two different markup languages that represent typographic style in text. Here they are:
Markdown
This is _italic_.HTML
Here is an <i>italic</i> word.For simplicity, our example HTML and Markdown grammars will only specify italics, but other text styles are of course possible.
Here’s the grammar for our simplified version of Markdown:
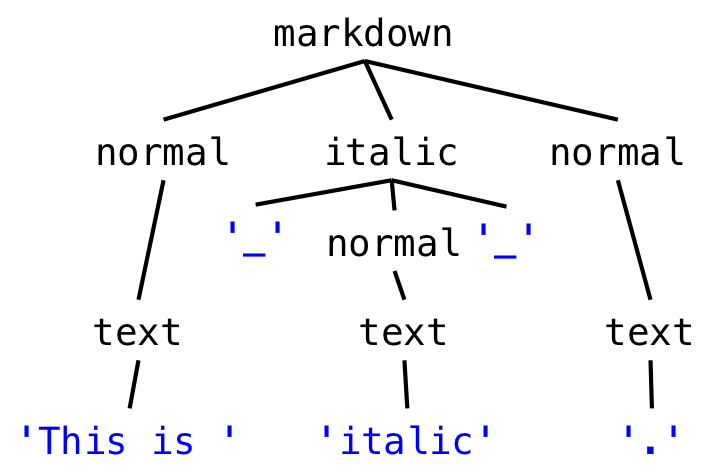
markdown ::= ( normal | italic ) *
italic ::= '_' normal '_'
normal ::= text
text ::= [^_]*Here’s the grammar for our simplified version of HTML:

html ::= ( normal | italic ) *
italic ::= '<i>' html '</i>'
normal ::= text
text ::= [^<>]*Regular Expressions
A regular grammar has a special property: by substituting every nonterminal (except the root one) with its righthand side, you can reduce it down to a single production for the root, with only terminals and operators on the right-hand side.
Our URL grammar was regular. By replacing nonterminals with their productions, it can be reduced to a single expression:
url ::= 'http://' ([a-z]+ '.')+ [a-z]+ (':' [0-9]+)? '/' The Markdown grammar is also regular:
markdown ::= ([^_]* | '_' [^_]* '_' )*But our HTML grammar can’t be reduced completely. By substituting righthand sides for nonterminals, you can eventually reduce it to something like this:
html ::= ( [^<>]* | '<i>' html '</i>' ) *
…but the recursive use of
html
on the righthand side can’t be eliminated, and can’t be simply replaced by a repetition operator either. So the HTML grammar is not regular.
The reduced expression of terminals and operators can be written in an even more compact form, called a
regular expression
. A regular expression does away with the quotes around the terminals, and the spaces between terminals and operators, so that it consists just of terminal characters, parentheses for grouping, and operator characters.
For example, the regular expression for our
markdown
format is just
([^_]*|_[^_]*_)*Regular expressions are also called regexes for short. A regex is far less readable than the original grammar, because it lacks the nonterminal names that documented the meaning of each subexpression. But a regex is fast to implement, and there are libraries in many programming languages that support regular expressions.
The regex syntax commonly implemented in programming language libraries has a few more special operators, in addition to the ones we used above in grammars. Here’s are some common useful ones:
. any single character
\d any digit, same as [0-9]
\s any whitespace character, including space, tab, newline
\w any word character, including letters and digits
\., \(, \), \*, \+, ...
escapes an operator or special character so that it matches literally
Using backslashes is important whenever there are terminal characters that would be confused with special characters. Because our
url
regular expression has
.
in it as a terminal, we need to use a backslash to escape it:
http://([a-z]+\.)+[a-z]+(:[0-9]+)/Using regular expressions in Java
Regular expressions (“regexes”) are widely used in programming, and you should have them in your toolbox.
In Java, you can use regexes for manipulating strings (see
String.split
,
String.matches
,
java.util.regex.Pattern
). They’re built-in as a first-class feature of modern scripting languages like Python, Ruby, and Javascript, and you can use them in many text editors for find and replace. Regular expressions are your friend! Most of the time. Here are some examples.
Replace all runs of spaces with a single space:
String singleSpacedString = string.replaceAll(" +", " ");Match a URL:
Pattern regex = Pattern.compile("http://([a-z]+\\.)+[a-z]+(:[0-9]+)?/");
Matcher m = regex.matcher(string);
if (m.matches()) {
// then string is a url
}Extract part of an HTML tag:
Pattern regex = Pattern.compile("<a href=['\"]([^']*)['\"]>");
Matcher m = regex.matcher(string);
if (m.matches()) {
String url = m.group(1);
// Matcher.group(n) returns the nth parenthesized part of the regex
}
Notice the backslashes in the URL and HTML tag examples.
In the URL example, we want to match a literal period
.
, so we have to first escape it as
\.
to protect it from being interpreted as the regex match-any-character operator, and then we have to further escape it as
\\.
to protect the backslash from being interpreted as a Java string escape character.
In the HTML example, we have to escape the quote mark
"
as
\"
to keep it from ending the string.
The frequency of backslash escapes makes regexes still less readable.
Context-Free Grammars
In general, a language that can be expressed with our system of grammars is called context-free. Not all context-free languages are also regular; that is, some grammars can’t be reduced to single nonrecursive productions. Our HTML grammar is context-free but not regular.
The grammars for most programming languages are also context-free. In general, any language with nested structure (like nesting parentheses or braces) is context-free but not regular. That description applies to the Java grammar, shown here in part:
statement ::=
'{' statement* '}'
| 'if' '(' expression ')' statement ('else' statement)?
| 'for' '(' forinit? ';' expression? ';' forupdate? ')' statement
| 'while' '(' expression ')' statement
| 'do' statement 'while' '(' expression ')' ';'
| 'try' '{' statement* '}' ( catches | catches? 'finally' '{' statement* '}' )
| 'switch' '(' expression ')' '{' switchgroups '}'
| 'synchronized' '(' expression ')' '{' statement* '}'
| 'return' expression? ';'
| 'throw' expression ';'
| 'break' identifier? ';'
| 'continue' identifier? ';'
| expression ';'
| identifier ':' statement
| ';'Summary
Machine-processed textual languages are ubiquitous in computer science. Grammars are the most popular formalism for describing such languages, and regular expressions are an important subclass of grammars that can be expressed without recursion.
The topics of today’s reading connect to our three properties of good software as follows:
-
Safe from bugs. Grammars and regular expressions are declarative specifications for strings and streams, which can be used directly by libraries and tools. These specifications are often simpler, more direct, and less likely to be buggy then parsing code written by hand.
-
Easy to understand. A grammar captures the shape of a sequence in a form that is easier to understand than hand-written parsing code. Regular expressions, alas, are often not easy to understand, because they are a one-line reduced form of what might have been a more understandable regular grammar.
-
Ready for change. A grammar can be easily edited, but regular expressions, unfortunately, are much harder to change, because a complex regular expression is cryptic and hard to understand.